[题目]已知:关于x的方程x2+2kx+k2﹣6＝0(1)证明:方程有两个不相等的实数根,(2)如果方程有一个根为2.试求2k2+8k+2018的值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知：关于x的方程x2+2kx+k2﹣6＝0

（1）证明：方程有两个不相等的实数根；

（2）如果方程有一个根为2，试求2k2+8k+2018的值．

【答案】（1）见解析；（2）2022.

【解析】

（1）计算判别式△＝24，然后根据判别式的意义得到结论；

（2）把x＝2代入方程得k2+4k＝2，再把2k2+8k+2018变形为2（k2+4k）+2018，然后利用整体代入的方法计算．

（1）证明：△＝（2k）2﹣4（k2﹣6）＝24＞0，

所以方程有两个不相等的实数根；

（2）把x＝2代入方程得4+4k+k2﹣6＝0，

所以k2+4k＝2，

所以2k2+8k+2018＝2（k2+4k）+2018＝2×2+2018＝2022．

练习册系列答案

假期总动员寒假作业假期最佳复习计划系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知△ABC的三边长分别是a，b，c，其中a=3，c=5，且关于x的一元二次方程x2-4x+b=0有两个相等的实数根，判断△ABC的形状.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．

最喜爱的项目类型频数分布表

项目类型	频数	频率
书法类	18	a
围棋类	14	0.28
喜剧类	8	0.16
国画类	b	0.20

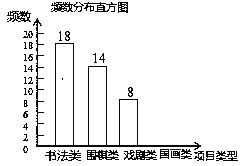
根据以上信息完成下列问题：

（1）直接写出频数分布表中a的值；

（2）补全频数分布直方图；

（3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

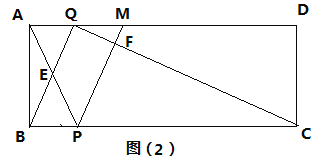
【题目】如图(1)，矩形ABCD，AB=2cm，AD=6cm，P、Q分别为两个动点，点P从B出发沿边BC运动，每秒1cm，点Q从B出发沿边B—C—D运动，每秒2cm.

（1）若P、Q两点同时出发，其中一点到达终点时另一点也随之停止，设△BPQ面积为S，时间为t秒，求S关于t的函数关系式及自变量的取值范围；

（2）若R为AD中点，连接RP、RQ，当以R、P、Q为顶点的三角形与△BPQ相似（含全等）时，求t的值；

（3）如图（2）M为AD边上一点，AM=2，点Q在1.5秒时便停止运动，点P继续在BC上运动，AP与BQ交于点E，PM交CQ于点F，设四边形QEPF的面积为y，求y的最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y（km）与已用时间x（h）之间的关系，则小敏、小聪行走的速度分别是（　　）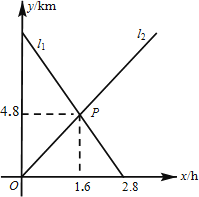

A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h