
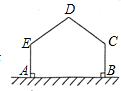
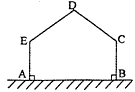
 用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为( )
用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为( )A、12
| ||
| B、12m2 | ||
C、24
| ||
| D、没有最大值 |
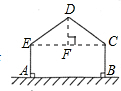 解:连接EC,作DF⊥EC,垂足为F
解:连接EC,作DF⊥EC,垂足为F| 1 |
| 2 |
| 3 |
3
| ||
| 4 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
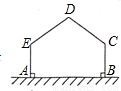
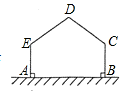 用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为
用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为 m2
m2 m2
m2查看答案和解析>>
科目:初中数学 来源:浙江省中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙教版九年级(上)质量检测数学试卷(10月份)(解析版) 题型:选择题
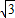 m2
m2 m2
m2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com