
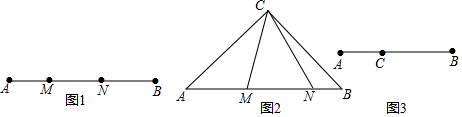
���� ��1���������������ù��ɶ������ɽ�����⣻
��2����ͼ������A��AD��AB����AD=BN��ֻҪ֤����ADC�ա�BNC���Ƴ�CD=CN����ACD=��BCN����֤����MDC�ա�MNC���ɵ�MD=MN���ɴ˼��ɽ�����⣻
��� ��1���⣺��MN�ʱ��BN=$\sqrt{M{N}^{2}-A{M}^{2}}$=4��
��BN�ʱ��BN=$\sqrt{A{M}^{2}+M{N}^{2}}$=$\sqrt{34}$��
��2��֤������ͼ������A��AD��AB����AD=BN
��AD=BN����DAC=��B=45�㣬AC=BC��
���ADC�ա�BNC��
��CD=CN����ACD=��BCN��
�ߡ�MCN=45�㣬
���DCA+��ACM=��ACM+��BCN=45��
���MCD=��BCM��
���MDC�ա�MNC��
��MD=MN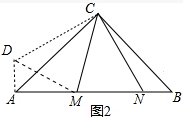
��Rt��MDA��AD2+AM2=DM2��
��BN2+AM2=MN2��
���M��N���߶�AB�Ĺ��ɷָ�㣮
��3������������AB�Ͻ�ȡCE=CA��
����AE�Ĵ�ֱƽ���ߣ�����ȡCF=CA��
������BF������BF�Ĵ�ֱƽ���ߣ���AB��D��
��D��Ϊ������ͼ3����ʾ��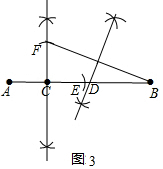
���� �������������ۺ���Ŀ���������¶��塰���ɷָ�㡱�����ɶ�������������λ�߶�����ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
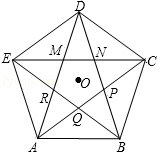 ��ͼ�������������ABCDE�ĸ����Խ���Χ��һ���µ������MNPQR��ͼ���кܶඥ��Ϊ36��ĵ��������Σ����ǰ����������γ�Ϊ���ƽ������Ρ����ƽ������εĵ�����֮��Ϊ$\frac{\sqrt{5}-1}{2}$����AB=$\frac{\sqrt{5}-1}{2}$����MN=$\sqrt{5}$-2��
��ͼ�������������ABCDE�ĸ����Խ���Χ��һ���µ������MNPQR��ͼ���кܶඥ��Ϊ36��ĵ��������Σ����ǰ����������γ�Ϊ���ƽ������Ρ����ƽ������εĵ�����֮��Ϊ$\frac{\sqrt{5}-1}{2}$����AB=$\frac{\sqrt{5}-1}{2}$����MN=$\sqrt{5}$-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x2=3x����x=3 | B�� | ��ax=ay����x=y | C�� | ��-$\frac{2}{3}$x=4����x=6 | D�� | ��$\frac{x}{a}$=$\frac{y}{a}$����x=y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
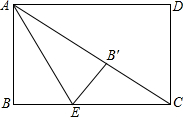 EΪ����ABCD��һ�㣬BE=1��CE=2��������ABCD��AE���ڵ�ֱ���۵���B��ǡ�����ڶԽ���AC�ϵĵ�B!�������BAE������ֵ��$\frac{\sqrt{3}}{3}$��
EΪ����ABCD��һ�㣬BE=1��CE=2��������ABCD��AE���ڵ�ֱ���۵���B��ǡ�����ڶԽ���AC�ϵĵ�B!�������BAE������ֵ��$\frac{\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com