
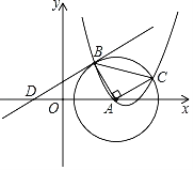
【题目】如图,已知的圆心为点![]() ,抛物线y=ax2﹣
,抛物线y=ax2﹣![]() x+c过点A,与
x+c过点A,与![]() 交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)求B、C点坐标和抛物线的解析式;
(2)直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;
(3)如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
【答案】(1)点B、C的坐标分别为(2,2)、(5,1),![]() ;(2)点E在抛物线上,理由见解析;(3)
;(2)点E在抛物线上,理由见解析;(3)![]() 或y=2x﹣1.
或y=2x﹣1.
【解析】
(1)根据题意,作出合适的辅助线,然后根据全等三角形的性质和判定可以得到点B和点C的坐标,然后将点B和C的坐标代入抛物线解析式,即可得到答案;
(2)根据(1)中的抛物线的解析式可以得到点D的坐标,从而可以求得直线BD的解析式,然后根据点E(与点D不重合)在该直线上,且AD=AE,即可得到点E的坐标,然后将点E的横坐标代入抛物线解析式,即可得到相应的纵坐标,即可判断点E是否在抛物线上;
(3)根据题意,画出相应的辅助线,然后利用分类讨论的方法可以求出满足条件的直线解析式.
解:(1)过点B、C分别作x轴的垂线交于点R、S,![]()
![]()
![]() ∠BAR+∠RBA=90°,∠BAR+∠CAS=90°,
∠BAR+∠RBA=90°,∠BAR+∠CAS=90°,
∴∠RAB=∠SCA,
又∵AB=AC,
∴![]() (AAS),
(AAS),
∴AS=BR,AR=CS,
∵B、C两点的纵坐标分别是2、1,![]()
∴AS=BR=2,AR=CS=1,
![]()
故点B、C的坐标分别为(2,2)、(5,1),
将点B、C坐标代入抛物线y=ax2﹣![]() x+c,
x+c,
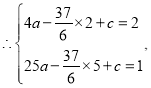
解得: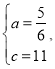
故抛物线的表达式为![]()
(2)∵直线y=kx+1经过点B(2,2),
∴2=2k+1,得![]()
即直线![]()
当y=0时,![]() 得x=﹣2,
得x=﹣2,
即点D的坐标为(﹣2,0),
∵点A、B、C、D的坐标分别为(3,0)、(2,2)、(5,1)、(﹣2,0),
∴![]() AD=5,
AD=5,
∵点E在直线BD上,
∴设E的坐标为![]() ,
,
∵AD=AE,
∴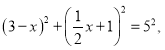
解得:x1=﹣2(舍去),x2=6,
∴点E(6,4),
当x=6时,![]()
∴点E在抛物线上;
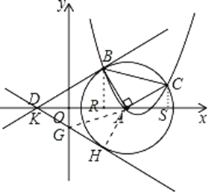
(3)①当切点在x轴下方时,
设直线y=k1x﹣1与⊙A相切于点H,
直线与x轴、y轴分别交于点K、G(0,﹣1),连接GA,
∵AR=1,![]() ∠BRA=90°,点A(3,0),点G(0,﹣1),
∠BRA=90°,点A(3,0),点G(0,﹣1),
∴AB=![]() AG=
AG=![]()
∴AH=AB=![]()
∵∠AHK=∠KOG=90°,∠HKA=∠OKG,
∴![]() ,
,
∴![]() ,
,
即: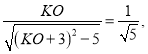
解得:KO=2或![]() (舍去),
(舍去),
经检验:![]() 符合题意,
符合题意,
∴点K的坐标为(﹣2,0),
把点K的坐标代入y=k1x﹣1,得
0=﹣2k1﹣1,得k1=![]() ,
,
∴直线的表达式为![]() ;
;
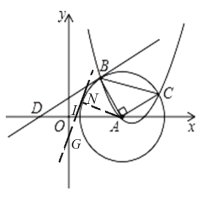
②当切点在x轴上方时,如图,切点为![]() ,
,
记![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]()
![]()
![]()
设![]() 则
则![]()
由勾股定理得:![]()
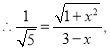
解得:![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
把![]() 代入y=k1x﹣1,
代入y=k1x﹣1,
![]()
![]()
![]() 此时切线为:
此时切线为:![]()
故满足条件的直线解析式为![]() 或y=2x﹣1.
或y=2x﹣1.


科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注,我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
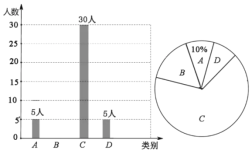
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”
(1)被调查的总人数是________人,扇形统计图中C部分所对应的扇形圆心角的度数为______;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中D类有______人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、情景问答三个项目,选拔比赛结束后,统计的这两位班主任成绩并制成了如图所示的条形统计图:
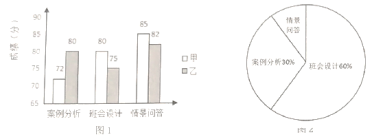
(1)乙班主任三个项目的成绩中位数是______________________;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图2所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
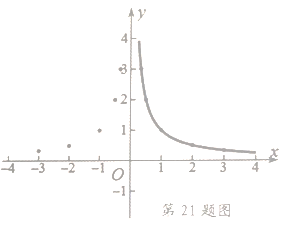
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,BC=6 cm.动点P在线段AC上以5 cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,以PD为一边向右作矩形PDEF,并且使DE=AD.设点P的运动时间为t s,矩形PDEF和△ABC重叠部分图形周长为y cm.
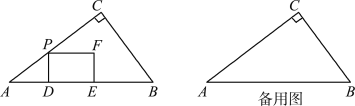
(1)当点F落在边BC上时,求t的值;
(2)求y与t之间的函数关系式;
(3)当矩形PDEF的面积被线段BC平分时,t=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
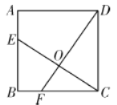
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的面积等于四边形
的面积等于四边形![]() 的面积,其中正确的有( )
的面积,其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
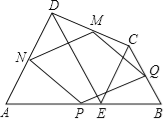
A.等腰梯形B.矩形C.菱形D.正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上,边长为![]() 的正方形和短边长为
的正方形和短边长为![]() 的矩形几何中心重合,如图①,当正方形和矩形都水平放置时,容易求出重叠面积
的矩形几何中心重合,如图①,当正方形和矩形都水平放置时,容易求出重叠面积![]() .
.
甲、乙、丙三位同学分别给出了两个图形不同的重叠方式;
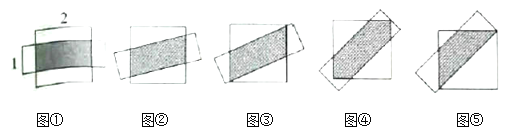
甲:矩形绕着几何中心旋转,从图②到图③的过程中,重叠面积![]() 大小不变.
大小不变.
乙:如图④,矩形绕着几何中心继续旋转,矩形的两条长边与正方形的对角线平行时,此时的重叠面积大于图③的重叠面积.
丙:如图⑤,将图④中的矩形向左上方平移,使矩形的一条长边恰好经过正方形的对角线,此时的重叠面积是![]() 个图形中最小的.
个图形中最小的.
下列说法正确的是( )
A.甲、乙、丙都对B.只有乙对C.只有甲不对D.甲、乙、丙都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com