
 如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017).
如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017). 分析 先求出直线l的解析式为y=$\frac{\sqrt{3}}{3}$x,设B点坐标为(x,1),根据直线l经过点B,求出B点坐标为($\sqrt{3}$,1),解Rt△A1AB,得出AA1=3,OA1=4,由平行四边形的性质得出A1C1=AB=$\sqrt{3}$,则C1点的坐标为(-$\sqrt{3}$,4),即(-$\sqrt{3}$×40,41);根据直线l经过点B1,求出B1点坐标为(4$\sqrt{3}$,4),解Rt△A2A1B1,得出A1A2=12,OA2=16,由平行四边形的性质得出A2C2=A1B1=4$\sqrt{3}$,则C2点的坐标为(-4$\sqrt{3}$,16),即(-$\sqrt{3}$×41,42);同理,可得C3点的坐标为(-16$\sqrt{3}$,64),即(-$\sqrt{3}$×42,43);进而得出规律,求得Cn的坐标是(-$\sqrt{3}$×4n-1,4n),即可求得C2017的坐标.
解答 解:∵直线l经过原点,且与y轴正半轴所夹的锐角为60°,
∴直线l的解析式为y=$\frac{\sqrt{3}}{3}$x,
∵AB⊥y轴,点A(0,1),
∴可设B点坐标为(x,1),
将B(x,1)代入y=$\frac{\sqrt{3}}{3}$x,得1=$\frac{\sqrt{3}}{3}$x,解得x=$\sqrt{3}$,
∴B点坐标为($\sqrt{3}$,1),AB=$\sqrt{3}$.在Rt△A1AB中,∠AA1B=90°-60°=30°,∠A1AB=90°,
∴AA1=$\sqrt{3}$AB=3,OA1=OA+AA1=1+3=4,
∵?ABA1C1中,A1C1=AB=$\sqrt{3}$,
∴C1点的坐标为(-$\sqrt{3}$,4),即(-$\sqrt{3}$×40,41);
由$\frac{\sqrt{3}}{3}$x=4,解得x=4$\sqrt{3}$,
∴B1点坐标为(4$\sqrt{3}$,4),A1B1=4$\sqrt{3}$.
在Rt△A2A1B1中,∠A1A2B1=30°,∠A2A1B1=90°,
∴A1A2=$\sqrt{3}$A1B1=12,OA2=OA1+A1A2=4+12=16,
∵?A1B1A2C2中,A2C2=A1B1=4$\sqrt{3}$,
∴C2点的坐标为(-4$\sqrt{3}$,16),即(-$\sqrt{3}$×41,42);
同理,可得C3点的坐标为(-16$\sqrt{3}$,64),即(-$\sqrt{3}$×42,43);
以此类推,则Cn的坐标是(-$\sqrt{3}$×4n-1,4n),
∴C2017的坐标是(-$\sqrt{3}$×42016,42017).
故答案为(-$\sqrt{3}$×42016,42017).
点评 本题考查了平行四边形的性质,解直角三角形以及一次函数的综合应用,先分别求出C1、C2、C3点的坐标,从而发现规律是解题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,4) | B. | (1,-3) | C. | (1,5) | D. | (-5,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
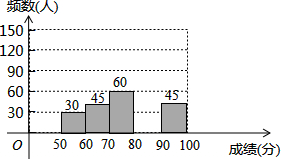 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
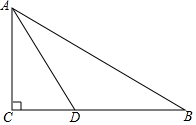 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
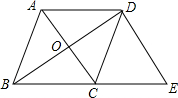 如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
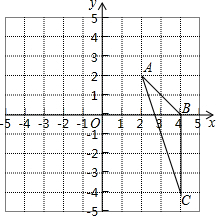 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
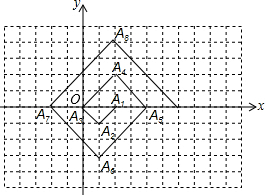 如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…都是斜边在x轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图所示规律,A2017的纵坐标为0.
如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…都是斜边在x轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图所示规律,A2017的纵坐标为0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com