练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知：点O是∠EPF的平分线上的一点，以点O为圆心的圆与角的两边分别交于点A、B和C、D。

    （1）求证： =；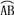

    （2）若角的顶点P在圆内，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省德州市2017-2018学年七年级上学期第一次月考数学试卷 题型：选择题

    下列各数中互为相反数的是（ ）

    A. 与0.2 B. 与－0.33 C. －2.25与 D. 5与－(－5)

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2018届九年级10月月考数学试卷 题型：选择题

    如图，已知AB是△ ABC外接圆的直径，∠ A=35°，则∠ B的度数是（　）

    A. 35° B. 45° C. 55° D. 65°

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市2017-2018学年八年级上学期第一次月考数学试卷 题型：选择题

    一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）

    A．108° B．90° C．72° D．60°

    查看答案和解析>>

    科目：初中数学 来源：江西省新余市2018届九年级上学期第一次阶段测试数学试卷 题型：解答题

    （11分）如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F. 点D、E的坐标分别为（0，6），（-4，0），连接PD，PE，DE.

    （1）请直接写出抛物线的解析式；

    （2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值. 进而猜想：对于任意一点P，PD与PF的差为定值. 请你判断该猜想是否正确，并说明理由；

    （3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE的周长最小时“好点”的坐标.

    查看答案和解析>>

    科目：初中数学 来源：江西省新余市2018届九年级上学期第一次阶段测试数学试卷 题型：填空题

    如图，P是抛物线y=2（x﹣2）2对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t= ．

    查看答案和解析>>

    科目：初中数学 来源：江西省新余市2018届九年级上学期第一次阶段测试数学试卷 题型：填空题

    方程x2=4x的解 __．

    查看答案和解析>>

    科目：初中数学 来源：山东省济宁市2018届九年级10月学业测试数学试卷 题型：解答题

    解方程：

    （1）； （2）．

    查看答案和解析>>

    科目：初中数学 来源：陕西省2017-2018学年七年级上学期第一次月考数学试卷 题型：计算题

    已知x，y为有理数，如果规定一种运算“*”，即x*y＝x-y＋1，试根据这种运算完成下列各题．

    (1)求2*4的值；

    (2)求(2*5)*(－3)的值；

    查看答案和解析>>

    同步练习册答案