
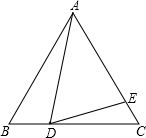
 如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.
如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.| 6 |
| 6-x |
| x |
| y |
| AB |
| DC |
| BD |
| CE |
| 6 |
| 6-x |
| x |
| y |
| 1 |
| 6 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?
建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?查看答案和解析>>
科目:初中数学 来源: 题型:
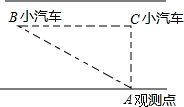 “交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?
“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com