
【题目】如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:AE=CF.
(2)求证:四边形BFDE为矩形.

【答案】(1)见解析;(2)见解析
【解析】
(1)由DE与AB垂直,BF与CD垂直,得到一对直角相等,再由四边形ABCD为平行四边形得到AD=BC,对角相等,利用AAS可得△ADE≌△CBF,由全等三角形的对应边相等即可得AE=CF;
(2)由平行四边形的对边平行得到DC与AB平行,得到∠CDE为直角,利用三个角为直角的四边形为矩形即可.
(1)∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°
∵四边形ABCD为平行四边形,
∴AD=BC, ∠A=∠C,
再在△ADE和△CBF中,
 ,
,
∴△ADE≌△CBF(AAS),
∴AE=CF.
(2)∵四边形ABCD为平行四边形,
∴CD∥AB,
∴∠CDE+∠DEB=180°,
∵∠DEB=90°,
∴∠CDE=90°,
∴∠CDE=∠DEB=∠BFD=90°,
则四边形BFDE为矩形.


科目:初中数学 来源: 题型:
【题目】如果两个角的差的绝对值等于![]() ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,
,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,![]() ,
,![]() ,
,![]() ,则
,则![]() 和
和![]() 互为反余角,其中
互为反余角,其中![]() 是
是![]() 的反余角,
的反余角,![]() 也是
也是![]() 的反余角.
的反余角.
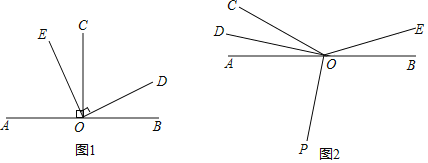
![]() 如图
如图![]() 为直线AB上一点,
为直线AB上一点,![]() 于点O,
于点O,![]() 于点O,则
于点O,则![]() 的反余角是______,
的反余角是______,![]() 的反余角是______;
的反余角是______;
![]() 若一个角的反余角等于它的补角的
若一个角的反余角等于它的补角的![]() ,求这个角.
,求这个角.
![]() 如图2,O为直线AB上一点,
如图2,O为直线AB上一点,![]() ,将
,将![]() 绕着点O以每秒
绕着点O以每秒![]() 角的速度逆时针旋转得
角的速度逆时针旋转得![]() ,同时射线OP从射线OA的位置出发绕点O以每秒
,同时射线OP从射线OA的位置出发绕点O以每秒![]() 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,
角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,![]() 与
与![]() 互为反余角
互为反余角![]() 图中所指的角均为小于平角的角
图中所指的角均为小于平角的角![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com