
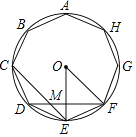
【题目】如图,⊙O的半径为2,正八边形ABCDEFGH内接于⊙O,对角线CE、DF相交于点M,则△MEF的面积是_____.
【答案】2﹣![]()
【解析】
设OE交DF于N,由正八边形的性质得出DE=FE,∠EOF=![]() =45°,
=45°,![]() ,由垂径定理得出∠OEF=∠OFE=∠OED,OE⊥DF,得出△ONF是等腰直角三角形,因此ON=FN=
,由垂径定理得出∠OEF=∠OFE=∠OED,OE⊥DF,得出△ONF是等腰直角三角形,因此ON=FN=![]() OF=
OF=![]() ,∠OFM=45°,得出EN=OE﹣OM=2﹣
,∠OFM=45°,得出EN=OE﹣OM=2﹣![]() ,证出△EMN是等腰直角三角形,得出MN=EN,得出MF=OE=2,由三角形面积公式即可得出结果.
,证出△EMN是等腰直角三角形,得出MN=EN,得出MF=OE=2,由三角形面积公式即可得出结果.
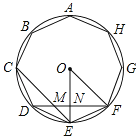
解:设OE交DF于N,如图所示:
∵正八边形ABCDEFGH内接于⊙O,
∴DE=FE,∠EOF=![]() =45°,
=45°,![]() ,
,
∴∠OEF=∠OFE=∠OED,OE⊥DF,
∴△ONF是等腰直角三角形,
∴ON=FN=![]() OF=
OF=![]() ,∠OFM=45°,
,∠OFM=45°,
∴EN=OE﹣OM=2﹣![]() ,∠OEF=∠OFE=∠OED=67.5°,
,∠OEF=∠OFE=∠OED=67.5°,
∴∠CED=∠DFE=67.5°﹣45°=22.5°,
∴∠MEN=45°,
∴△EMN是等腰直角三角形,
∴MN=EN,
∴MF=MN+FN=ON+EN=OE=2,
∴△MEF的面积=![]() MF×EN=
MF×EN=![]() ×2×(2﹣
×2×(2﹣![]() )=2﹣
)=2﹣![]() ;
;
故答案为:2﹣![]() .
.


科目:初中数学 来源: 题型:
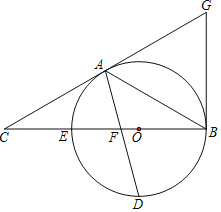
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC,
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)过点B作⊙O的切线交CA的延长线于G,如果连接AE,将线段AC以直线AE为对称轴作对称线段AH,点H正好落在⊙O上,连接BH,求证:四边形AHBG为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.
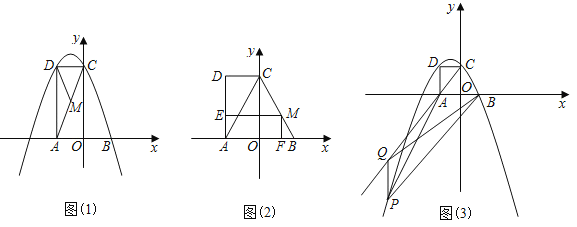
(1)求经过B、C、D三点的抛物线解析式;
(2)点P在(1)中的抛物线上,当M为AC中点时,若△PAM≌△PDM,求点P的坐标;
(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;
(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可销售出20件,每件盈利40元,为扩大销售盈利减小库存,商场决定采取适当的降价措施,但要求每件盈利不少于20元,经调查发现。若每件衬衫每降价1元,则商场每天可多销售2件.
(1)若每件衬衫降价4元,则每天可盈利多少元?
(2)若商场平均每天盈利1200元。则每件衬衫应降价多少元?
(3)若商场为增加效益最大化,求每件衬衫应降价多少元时,商场平均每天盈利最多?每天最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会提出了要坚定实施七大战略,某数学兴趣小组从中选取了四大战略进行调查,A:科教兴国战略,B:人才强国战略,C:创新驱动发展战略,D:可持续发展战略,要求被调查的每位学生只能从中选择一个自已最关注的战略,根据调查结果,该小组绘制了如图所示的两幅不完整的统计图,请你根据统计图中提供的信息,解答下列问题:
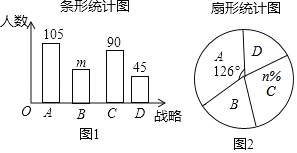
(1)求本次抽样调查的学生人数;
(2)求出统计图中m、n的值;
(3)在扇形统计图中,求战略B所在扇形的圆心角度数;
(4)若该校有3000名学生,请估计出选择战略A和B共有的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
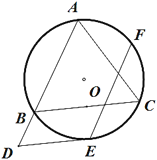
【题目】如图,△ABC内接于⊙O,AB=AC=10,BC=12,点E是弧BC的中点.
(1)过点E作BC的平行线交AB的延长线于点D,求证:DE是⊙O的切线.
(2)点F是弧AC的中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABCD=9,则k值为( )
OC,S四边形ABCD=9,则k值为( )
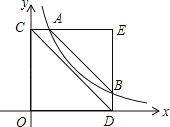
A.8B.10C.12D.16.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com