
如图有下面三个判断:①∠A=∠F,②∠C=∠D,③∠1=∠2,请你用其中两个作为条件,余下一个作为结论,编一道证明题并写出证明过程.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是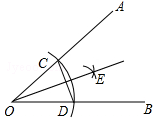
A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
填写推理理由(1×10=10分)
如图,已知AB∥CD ,∠1=∠2,∠3=∠4,试说明AD∥BE
解:∵AB∥CD(已知)
∴∠4=∠_____( )
∵∠3=∠4(已知)
∴∠3=∠_____( )
∵∠1=∠2(已知)
∴∠ CAE+ =∠CAE+
即 ∠_____ =∠_____
∴∠3=∠_____
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.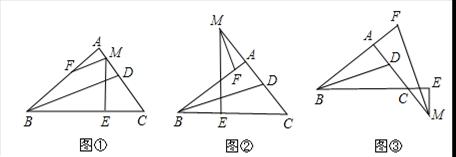
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com