
【题目】在某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答)
科目:初中数学 来源: 题型:
【题目】育英学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张参加某公司招聘测试,他的笔试、面试、计算机操作得分分别为80分,85分,90分,若三项得分依次按照25%、20%、55%确定成绩,则小王的成绩是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
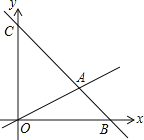
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光的速度约为3×105km/s,以太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年的时间才能到达地球.若一年以3×107s计算,则这颗恒星到地球的距离是 km.(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
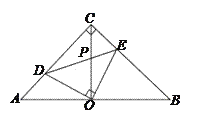
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D,E分别在AC,BC边上,且∠DOE=90°,DE交OC于P,下列结论正确的共有( )
①图中的全等三角形共有3对;②AD=CE;③∠CDO=∠BEO;④OC=DC+CE;⑤△ABC的面积是四边形DOEC面积的2倍。
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 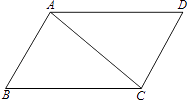
(1)试说明AD∥BC.
(2)若AB与CD也平行,求∠D的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com