练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
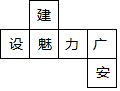
    16．如图是一个正方体的表面展开图，则原正方体中与“魅”字所在的面相对的面上标的字是（　　）
    A．建B．力C．广D．安

    分析 正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．

    解答 解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
    “建”与“安”是相对面，
    “设”与“力”是相对面，
    “魅”与“广”是相对面．
    故选：C．

    点评 本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．如图，一次函数y=ax+b（a≠0）与二次函数y=ax2+bx（a≠0）图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．用两种正多边形镶嵌，不能与正三角形匹配的正多边形是（　　）
    A．正方形B．正六边形C．正八边形D．正十二边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4$\sqrt{2}$，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．
    （1）求抛物线C的函数表达式；
    （2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．
    （3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．在△ABC中，∠C=90°，a、b分别是∠A、∠B所对的两条直角边，c是斜边，则有（　　）是正确的．
    A．sinA=$\frac{c}{a}$B．cosB=$\frac{b}{c}$C．sinB=$\frac{b}{a}$D．tanA=$\frac{a}{b}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

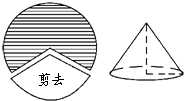    1．如图，将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形，用剩下的扇形围成一个圆锥的侧面（接缝忽略不计），这个圆锥的高是（　　）
    A．12cmB．8cmC．20cmD．18cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

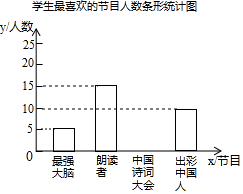    8．为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：
                    学生最喜爱的节目人数统计表
     节目 人数（名） 百分比
     最强大脑 5 10%
     朗读者 15 b%
     中国诗词大会 a 40%
     出彩中国人 10 20%
    根据以上提供的信息，解答下列问题：
    （1）x=50，a=20，b=30；
    （2）补全上面的条形统计图；
    （3）若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

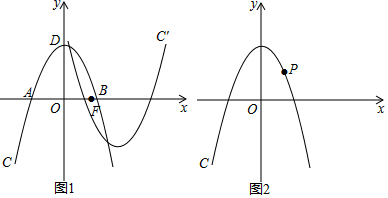
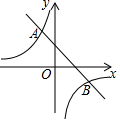    5．如图，一次函数y=k1x+b（k1≠0）与反比例函数y=$\frac{k_2}{x}$（k2≠0）的图象交于点A（-1，2），B（m，-1）．
    （1）求这两个函数的表达式；
    （2）在x轴上是否存在点P（n，0）（n＞0），使△ABP为等腰三角形？若存在，求n的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，直线AB，CD分别与⊙O相切于B，D两点，且AB⊥CD，垂足为P，连接BD，若BD=4，则阴影部分的面积为2π-4．

    查看答案和解析>>

    同步练习册答案