
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 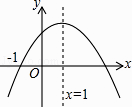
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,AC=6,BD=10,动点P从B出发以每秒1个单位的速度沿射线BD匀速运动,动点Q从D出发以相同速度沿射线DB匀速运动,设运动时间为t秒.
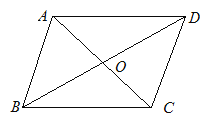
(1)当t =2时,证明以A、P、C、Q为顶点的四边形是平行四边形.
(2)当以A、P、C、Q为顶点的四边形为矩形时,直接写出t的值.
(3)设PQ=y,直接写出y与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
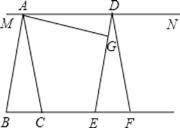
【题目】如图所示,将![]() 沿直线BC方向平移
沿直线BC方向平移![]() 的位置,G是DE上一点,连接AG,过点A、D作直线MN.
的位置,G是DE上一点,连接AG,过点A、D作直线MN.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断AG与DE的位置关系,并证明你的结论.
,判断AG与DE的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
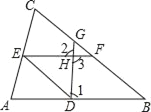
【题目】完成下面的证明过程
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的数阵是由77个偶数排成:
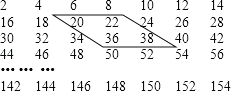
(1)如图中任意作一个平行四边形框,设左上角的数为x,那么其他3个数从小到大可分别表示为 .
(2)小红说这4个数的和是292,能求出这4个数吗?若存在,请求出这4个数.不存在说明理由.
(3)小明说4个数的和是420,存在这样的数吗?若存在,请求出这4个数,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为2014(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 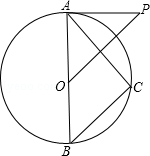
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com