
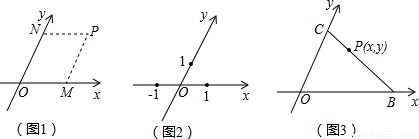
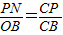 、
、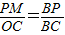 ;再由线段间的和差关系求得PC+BP=BC知
;再由线段间的和差关系求得PC+BP=BC知 ;
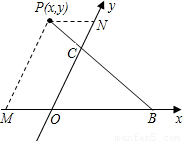
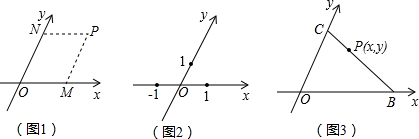
;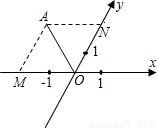 解:(1)作AM∥y轴,AM与x轴交于点M,AN∥x轴,AN与y轴交于点N,
解:(1)作AM∥y轴,AM与x轴交于点M,AN∥x轴,AN与y轴交于点N,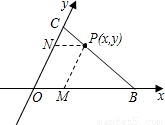
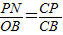 ,即
,即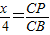 ;
;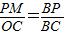 ,即
,即 ;
;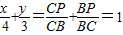 ,
,
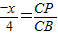 ,
,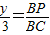 .
. .
.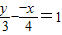 ,即
,即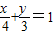 .
.

科目:初中数学 来源: 题型:
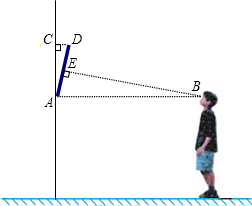 知装饰画的高度AD为0.66米,
知装饰画的高度AD为0.66米,查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届广东省九年级第一次月考考试数学卷 题型:选择题
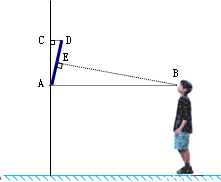
我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com