
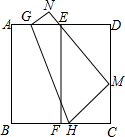
 如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N
如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N分析 (1)利用翻折变换的性质结合勾股定理表示出CH的长即可;
(2)首先得出△EDM∽△MCH,进而求出MC的长,再利用△NEG∽△DEM,求出NG的长,再利用勾股定理得出GH的长.
解答 解:(1)∵CM=x,BC=6,
∴设HC=y,则BH=HM=6-y,
故y2+x2=(6-y)2,
整理得:y=-$\frac{1}{12}$x2+3,
∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,
∴△EDM∽△MCH,
∴$\frac{ED}{MC}$=$\frac{DM}{CH}$,
∴$\frac{3}{x}$=$\frac{6-x}{HC}$,
解得:HC=-$\frac{1}{3}$x2+2x,
故答案为:-$\frac{1}{12}$x2+3或-$\frac{1}{3}$x2+2x;
(2)方法一:
∵四边形ABCD为正方形,
∴∠B=∠C=∠D=90°,
设CM=x,由题意可得:ED=3,DM=6-x,∠EMH=∠B=90°,
故∠HMC+∠EMD=90°,
∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,
∴△EDM∽△MCH,
∴$\frac{ED}{MC}$=$\frac{DM}{CH}$,
即$\frac{3}{x}$=$\frac{6-x}{-\frac{1}{12}{x}^{2}+3}$,
解得:x1=2,x2=6(不合题意舍去),
∴CM=2,
∴DM=4,
∴在Rt△DEM中,由勾股定理得:EM=5,
∴NE=MN-EM=6-5=1,
∵∠NEG=∠DEM,∠N=∠D,
∴△NEG∽△DEM,
∴$\frac{NE}{DE}$=$\frac{NG}{DM}$,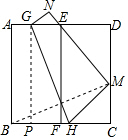
∴$\frac{1}{3}$=$\frac{NG}{4}$,
解得:NG=$\frac{4}{3}$,
由翻折变换的性质,得AG=NG=$\frac{4}{3}$,
过点G作GP⊥BC,垂足为P,
则BP=AG=$\frac{4}{3}$,GP=AB=6,
当x=2时,CH=-$\frac{1}{12}$x2+3=$\frac{8}{3}$,
∴PH=BC-HC-BP=6-$\frac{8}{3}$-$\frac{4}{3}$=2,
在Rt△GPH中,GH=$\sqrt{G{P}^{2}+P{H}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
方法二:有上面方法得出CM=2,
连接BM,
可得BM⊥GH,
则可得∠PGH=∠HBM,
在△GPH和△BCM中
$\left\{\begin{array}{l}{∠HGP=∠CBM}\\{GP=BC}\\{∠GPH=∠C}\end{array}\right.$,
∴△GPH≌△BCM(SAS),
∴GH=BM,
∴GH=BM=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
点评 此题主要考查了翻折变换的性质以及正方形的性质、相似三角形的判定与性质和勾股定理,正确应用相似三角形的判定与性质是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 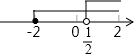 | B. |  | C. | 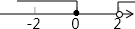 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
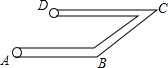 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )| A. | AB∥BC | B. | BC∥CD | C. | AB∥DC | D. | AB与CD相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com