
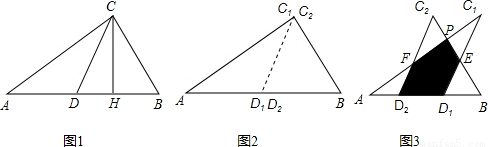
 AB=5.
AB=5. AC•BC=
AC•BC= AB•CH,
AB•CH, ×6×8=
×6×8=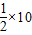 CH,
CH,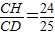 ,
, .
.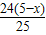 ,
, ×BD1×h=
×BD1×h=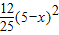 .
. ,cos∠B=
,cos∠B= ,
, x,PF=
x,PF= x,
x,
 =
= x2.
x2. S△ABC-
S△ABC-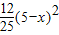 -=
-=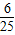 x2,
x2,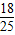 x2+
x2+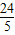 x;
x;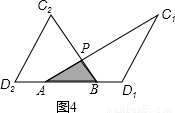
 =
= ,cos∠PBA=
,cos∠PBA= =
= ,
, ,PB=
,PB= (10-x),
(10-x), ×PA×PB=
×PA×PB= ×
×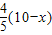 ×
× (10-x),
(10-x), (10-x)2.
(10-x)2.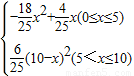
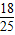 x2+
x2+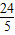 x=3,
x=3,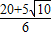 >5(舍去),x2=
>5(舍去),x2=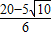 ;
;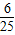 (10-x)2=3,
(10-x)2=3, >(舍去),x2=10-
>(舍去),x2=10- ;
;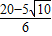 或x=10-
或x=10- 时,重叠部分的面积等于3.
时,重叠部分的面积等于3.

科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》常考题集(24):34.4 二次函数的应用(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.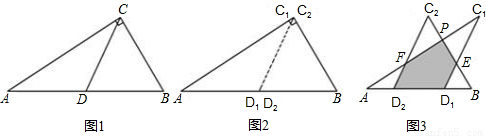
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(41):2.4 二次函数的应用(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年广东省汕头市龙湖区中考数学模拟试卷(解析版) 题型:解答题
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com