
分析 先算括号里面的,再算除法,最后求出x的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}-1-{x}^{2}}{x(x-1)}$•x
=$\frac{-1}{x(x-1)}$•x
=$\frac{1}{1-x}$,
将x=2×$\frac{1}{2}$+$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1+1=2代入得,
原式=$\frac{1}{1-2}$=-1.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 100(1+x) | B. | 100(1+x)2 | C. | 100(1+x2) | D. | 100(1+2x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲,乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图表示,当甲车出发$\frac{3}{2}$h时,两车相距350km.
在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲,乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图表示,当甲车出发$\frac{3}{2}$h时,两车相距350km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
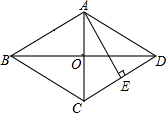 如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.
如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )| A. | $y=\frac{20}{x}$ | B. | $y=-\frac{20}{x}$ | C. | $y=\frac{12}{x}$ | D. | $y=-\frac{12}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
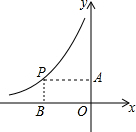 如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.
如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com