
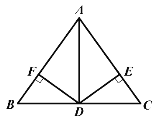
【题目】如图,D是△ABC边BC的中点,DE⊥AC于点E,DF⊥AB于点F,若DE=DF
(1)证明:△ABC的等腰三角形
(2)连接AD,若AB=5,BC=8,求DE的长
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)求出BD=CD,∠DEB=∠DFC=90°,根据HL证出Rt△BDE≌Rt△CDF,得出∠B=∠C,即可得出结论;
(2)由等腰三角形的性质得出AD⊥BC,由勾股定理求出AD,根据面积法求出DE即可.
(1)证明:∵D是BC的中点,
∴BD=CD,
∵DF⊥AB,DE⊥AC,
∴∠DFB=∠DEC=90°,
在Rt△BDF与Rt△CDE中,
![]() ,
,
∴Rt△BDF≌Rt△CDE(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:由(1)得:AB=AC,
∵D是△ABC边BC的中点,
∴AD⊥BC,CD=![]() BC=4,
BC=4,
∴AD=![]() =3,
=3,
∵△ACD的面积=![]() AC×DE=
AC×DE=![]() CD×AD,
CD×AD,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
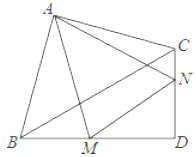
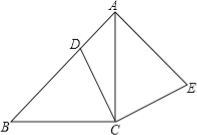
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
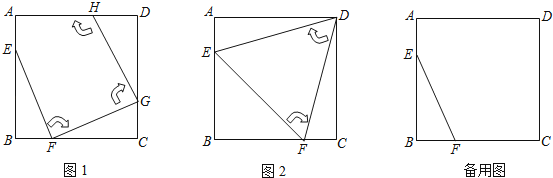
【题目】如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
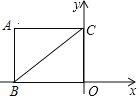
【题目】如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
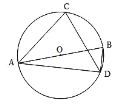
【题目】如图, AB 是⊙O 的直径,点 C 和点 D 是⊙O 上两点,连接 AC 、CD 、 BD ,若 CA= CD,∠ ACD = 80° ,则∠ CAB =______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应问题:
材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在求解某些特殊方程时,利用换元法常常可以达到转化的目的,例如在求解一元四次方程![]() ,就可以令
,就可以令![]() ,则原方程就被换元成
,则原方程就被换元成![]() ,解得 t 1,即
,解得 t 1,即![]() ,从而得到原方程的解是 x 1
,从而得到原方程的解是 x 1
材料二:杨辉三角形是中国数学上一个伟大成就,在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现,它呈现了某些特定系数在三角形中的一种有规律的几何排列,下图为杨辉三角形:

……………………………………
(1)利用换元法解方程:![]()
(2)在杨辉三角形中,按照自上而下、从左往右的顺序观察, an 表示第 n 行第 2 个数(其中 n≥4),bn 表示第 n 行第 3 个数,![]() 表示第
表示第![]() 行第 3 个数,请用换元法因式分解:
行第 3 个数,请用换元法因式分解:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)已知直线![]() 与抛物线
与抛物线![]() 相交于抛物线的顶点
相交于抛物线的顶点![]() 和另一点
和另一点![]() ,点
,点![]() 在第四象限.
在第四象限.
![]() 若点
若点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 过点
过点![]() 作
作![]() 轴的平行线与抛物线
轴的平行线与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com