
【题目】公园里有甲、乙两组游客正在做团体游戏,两组游客的年龄如下:(单位:岁)
甲组:13,13,14,15,15,15,15,16,17,17;
乙组:3,4,4,5,5,6,6,6,54,57.
我们很想了解一下甲、乙两组游客的年龄特征,请你运用“数据的代表”的有关知识对甲、乙两组数据进行分析,帮我们解决这个问题.
【答案】因为平均数受到极端值的影响很大,所以其中能较好反映乙组游客年龄特征的是:中位数、众数.
【解析】
根据平均数、中位数和众数的定义分别求出两组数据的平均数、中位数、众数和方差,再分析即可.
甲组游客的平均年龄是(13+13+14+15+15+15+15+16+17+17)÷10=15(岁),
中位数=(15+15)÷2=15(岁),众数是15岁,
甲组的方差是:![]() [2(13﹣15)2+(14﹣15)2+4(15﹣15)2+(16﹣15)2+2(17﹣15)2]=1.8;
[2(13﹣15)2+(14﹣15)2+4(15﹣15)2+(16﹣15)2+2(17﹣15)2]=1.8;
甲的平均数、众数和中位数都能反应甲组游客年龄特征;
乙组游客的平均年龄是(3+4+4+5+5+6+6+6+54+57)÷10=15(岁),
中位数是=![]() =5.5(岁),众数是6岁,
=5.5(岁),众数是6岁,
则乙组的方差是:![]() [(3﹣15)2+2(4﹣15)2+2(5﹣15)2+3(6﹣15)2+(54﹣15)2+(57﹣15)2]=590,
[(3﹣15)2+2(4﹣15)2+2(5﹣15)2+3(6﹣15)2+(54﹣15)2+(57﹣15)2]=590,
因为平均数受到极端值的影响很大,所以其中能较好反映乙组游客年龄特征的是:中位数、众数.


科目:初中数学 来源: 题型:
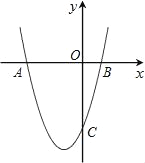
【题目】如图,抛物线y=x2+bx+c经过点A(﹣4,0)和C点(0,﹣4),与x轴另一个交点为B.
(1)求此二次函数的解析式和顶点D的坐标;
(2)求出A、B两点之间的距离;
(3)直接写出当y>﹣4时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
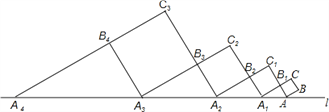
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
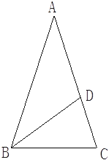
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,
(1)求证:△ABC∽△BCD;
(2)若BC=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
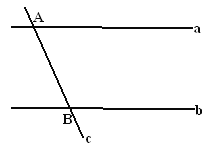
【题目】如图,a、b、c是三条公路,且a∥b,加油站M到三条公路的距离相等.(1)确定加油站M的位置.(保留作图痕迹,不写作法)
(2)一辆汽车沿公路c由A驶向B,行使到AB中点时,司机发现油料不足,仅剩15升汽油,需要到加油站加油,已知从AB中点有路可直通加油站,若AB相距200千米,汽车每行使100千米耗油12升,请判断这辆汽车能否顺利到达加油站?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
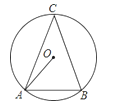
【题目】如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
(3)若点C平分优弧AB,且BC2=3OA2 ,试求α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
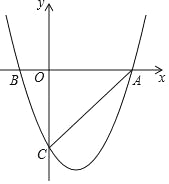
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,连接AC,A(3,0),AC=3![]() .
.
(1)求抛物线的函数解析式,并直接写出顶点坐标;
(2)点P是第四象限内抛物线上一点,过点P作PQ⊥AC于Q,直接写出当线段PQ长度最大时,点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com