
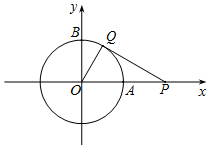
 以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.;如图,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时Q走过的路程弧$\widehat{BQ}$的长为 $\frac{π}{6}$;
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.;如图,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时Q走过的路程弧$\widehat{BQ}$的长为 $\frac{π}{6}$;分析 (1)先求出∠BOQ,再用含30°角的直角三角形的性质求出OC,CQ即可;
(2)用三角函数先求出∠OPQ,再求出∠OQP的度数即可得出结论;
(3)先求出Q点的运动速度,利用垂径定理,勾股定理可以解决.
解答 解:(1)如图1,过点Q作QC⊥OA,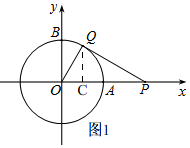 设∠BOQ=n,
设∠BOQ=n,
∵Q走过的路程弧$\widehat{BQ}$的长为 $\frac{π}{6}$,
∴$\frac{nπ•1}{180}$=$\frac{π}{6}$,
∴n=30°,
∴∠BOQ=30°,
在Rt△OCQ中,∠COQ=90°-30°=60°,OQ=1,
∴OC=$\frac{1}{2}$,CQ=$\frac{\sqrt{3}}{2}$,
∴Q($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(2)如图1,∵P(2,0),
∴OP=2,
∴CP=OP-OC=$\frac{3}{2}$,
在Rt△COP中,tan∠OPQ=$\frac{CQ}{CP}=\frac{\frac{\sqrt{3}}{2}}{\frac{3}{2}}$=$\frac{\sqrt{3}}{3}$,
∴锐角∠CPQ=30°,
∴∠OPQ+∠POQ=90°,
∴∠OQP=90°,
∴OQ⊥PQ,
∵点Q在⊙O上,
∴PQ与⊙O相切;
(3)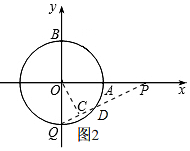 由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,
由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,
若Q按照原来的方向和速度继续运动,那么再过5秒,则点Q再绕点O顺时针旋转150°,
即:Q点落在⊙O与y轴负半轴的交点处(如图2)
.设直线PQ与⊙O的另外一个交点为D,
过O作OC⊥QD于点C,则C为QD的中点.
∵∠QOP=90°,OQ=1,OP=2,
∴QP=$\sqrt{5}$,
∵$\frac{1}{2}$OQ•OP=$\frac{1}{2}$QP•OC,
∴OC=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵OC⊥QD,OQ=1,
∴QC=$\frac{\sqrt{5}}{5}$,
∴QD=$\frac{2\sqrt{5}}{5}$.
点评 此题是圆的综合题,主要考查了弧长公式,切线的判定,垂径定理,勾股定理,锐角三角函数,解本题的关键是判断出点PQ是⊙O的切线和点Q再过5秒时的位置,是一道涉及知识点比较多的中考常考题.


科目:初中数学 来源: 题型:填空题
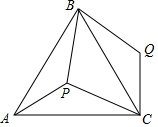 如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数150°.
如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数150°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
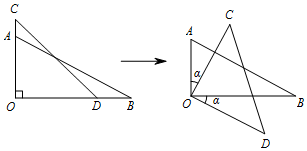 将两块直角三角尺的直角顶点重合为如图所示的位置,△COD为等腰直角三角形,当△COD绕点O顺时针旋转α度(0<α<90),∠COB:∠BOD=3:2时,则∠BOC=54°.
将两块直角三角尺的直角顶点重合为如图所示的位置,△COD为等腰直角三角形,当△COD绕点O顺时针旋转α度(0<α<90),∠COB:∠BOD=3:2时,则∠BOC=54°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com