
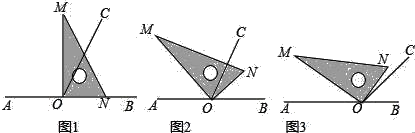
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
【答案】25° 40° 25°
【解析】
(1)根据∠MON和∠BOC的度数可以得到∠MOC的度数;
(2)根据OC平分∠MOB,∠BOC=65°可以求得∠BOM的度数,由∠MON=90°,可得∠BON的度数,继而可得∠CON的度数;
(3)由∠NOC=5°,∠BOC=65°,∠MON=90°结合平角的定义即可求得.
(1)∠MOC=∠MON﹣∠BOC=90°﹣65°=25°,
故答案为:25°;
(2)∵OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=2×65°=130°,
∴旋转角∠BON=∠MOB﹣∠MON=130°﹣90°=40°,
∠CON=∠BOC﹣∠BON=65°﹣40°=25°,
故答案为:40°,25°;
(3)∵∠NOC=5°,∠BOC=65°,
∴∠BON=∠NOC+∠BOC=70°,
∵点O为直线AB上一点,
∴∠AOB=180°,
∵∠MON=90°,
∴∠AOM=∠AOB﹣∠MON﹣∠BON=180°﹣90°﹣70°=20°.


科目:初中数学 来源: 题型:
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
A | 4.5≤x<5.5 |
B | 5.5≤x<6.5 |
C | 6.5≤x<7.5 |
D | 7.5≤x<8.5 |
E | 8.5≤x<9.5 |
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值 ![]()
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?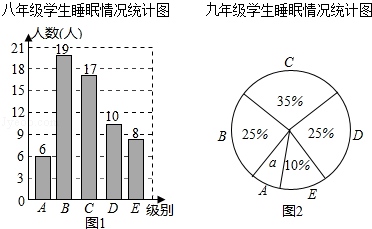
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
如图,将一个矩形纸片ABCD,放置在平面直角坐标系中,A(0,0),B(4,0),D(0,3),M是边CD上一点,将△ADM沿直线AM折叠,得到△ANM.
(Ⅰ)当AN平分∠MAB时,求∠DAM的度数和点M的坐标;
(Ⅱ)连接BN,当DM=1时,求△ABN的面积;
(Ⅲ)当射线BN交线段CD于点F时,求DF的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长MN与x轴交于P点,于是出现了Rt△NAP,…
小雨:我和你想的不一样,我过点N作y轴的平行线,出现了两个Rt△NAP,…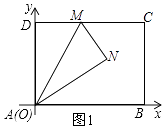
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( ) 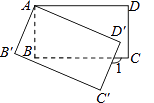
A.68°
B.20°
C.28°
D.22°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(Ⅰ)被抽样调查的学生有 人,并补全条形统计图 ;
(Ⅱ)每天户外活动时间的中位数是 (小时);
(Ⅲ)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有 人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com