
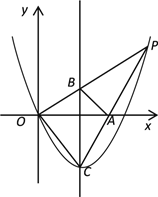
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
【答案】(1) y=x2-2x;(2)BC=m-1;(3) P的坐标为(![]() )
)
【解析】分析:(1)由对称轴公式,以及已知顶点C坐标,利用待定系数法确定出解析式即可;
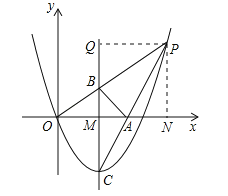
(2)设出P坐标,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N,表示出PN,ON,OM,利用比例表示出BM,进而表示出BC即可;
(3)设出P坐标,由两三角形面积相等得到AC=AP,过点P作PQ⊥BC交BC于点Q,列出关于t的方程,求出方程的解确定出t的值,即可求出P坐标.
详解:(1)∵抛物线y=ax2+bx的顶点为C(1,﹣1),∴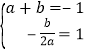 ,解得:
,解得:![]() ,∴抛物线的表达式为:y=x2﹣2x;
,∴抛物线的表达式为:y=x2﹣2x;
(2)∵点P的横坐标为m,∴点P的纵坐标为:m2﹣2m,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N.∵P是抛物线上位于第一象限内的一点,∴PN=m2﹣2m,ON=m,OM=1,由![]() =
=![]() ,得:
,得:![]() =
=![]() ,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
(3)令P(t,t2﹣2t).∵△ABP的面积等于△ABC的面积,∴AC=AP,过点P作PQ⊥BC交BC于点Q,∴CM=MQ=1,可得:t2﹣2t=1,解得:t=1+![]() (t=1﹣
(t=1﹣![]() 舍去),∴P的坐标为(1+
舍去),∴P的坐标为(1+![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】下列说法:①平角就是一条直线;②直线比射线线长;③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个;④连接两点的线段叫两点之间的距离;⑤两条射线组成的图形叫做角;⑥一条射线把一个角分成两个角,这条射线是这个角的角平分线,其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售(结果用含m,n的式子表示)
(1)求售出100个手机充电宝的总售价为多少元?
(2)由于开学临近,小丽在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.(注:售价的8折即按原售价的80%出售)
①她的总销售额是多少元?
②假如不采取降价销售,且也全部售完,她将比实际销售多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地重视生态建设,大力发展旅游业,各地旅游团纷沓而至,某旅游团上午6时从旅游馆出发,乘汽车到距离![]() 的旅游景点观光,该汽车离旅游馆的距离
的旅游景点观光,该汽车离旅游馆的距离![]() 与时间
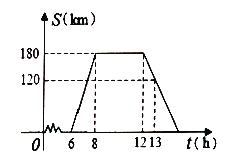
与时间![]() 的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)求该团旅游景点时的平均速度是多少?
(2)该团在旅游景点观光了多少小时?
(3)求该团返回到宾馆的时刻是几时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
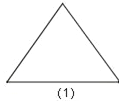
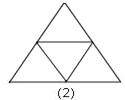
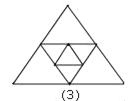
按上面方法继续下去,第20个图有_____个三角形;第n个图中有_____个三角形.(用n的代数式表示结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
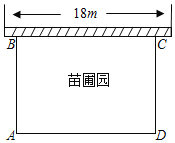
【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
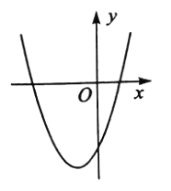
【题目】在平面直角坐标系中,二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() ,
,![]() 是该二次函数图象上的两点,其中
是该二次函数图象上的两点,其中![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ![]() B.
B. ![]() C. 函数
C. 函数![]() 的最小值是
的最小值是![]() D. 函数
D. 函数![]() 的最小值是
的最小值是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com