练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2012•河源）如图，连接在一起的两个正方形的边长都为1cm，一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动．①第一次到达G点时移动了
    7
    7
    cm；②当微型机器人移动了2012cm时，它停在
    E
    E
    点．
    分析：①结合图形，找出第一次到达G点时走过的正方形的边长数即可得解；
    ②根据移动一圈的路程为8cm，用2012除以8，余数是几就落在从A开始所走的距离，然后即可找出最后停的点．
    解答：解：①由图可知，从A开始，第一次移动到G点，共经过AB、BC、CD、DE、EF、FC、CG七条边，
    所以共移动了7cm；
    ②∵机器人移动一圈是8cm，
    2012÷8=251…4，
    ∴移动2012cm，是第251圈后再走4cm正好到达E点．
    故答案为：7，E．
    点评：本题考查的是循环的规律，要注意所求的值经过了几个循环，然后便可得出结论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

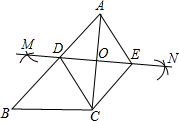    （2012•河源）如图，已知△ABC，按如下步骤作图：
    ①分别以A、C为圆心，以大于
    12
    AC的长为半径在AC两边作弧，交于两点M、N；
    ②连接MN，分别交AB、AC于点D、O；
    ③过C作CE∥AB交MN于点E，连接AE、CD．
    （1）求证：四边形ADCE是菱形；
    （2）当∠ACB=90°，BC=6，△ADC的周长为18时，求四边形ADCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

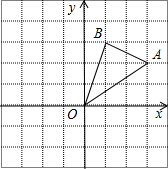    （2012•河源）如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接填写答案）
    （1）点A关于点O中心对称的点的坐标为
    （-3，-2）
    （-3，-2）
    ；
    （2）点A1的坐标为
    （-2，3）
    （-2，3）
    ；
    （3）在旋转过程中，点B经过的路径为弧BB1，那么弧BB1的长为
    		10
    2
    π
    		10
    2
    π
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•河源）如图，AC是⊙O的直径，弦BD交AC于点E．
    （1）求证：△ADE∽△BCE；
    （2）如果AD2=AE•AC，求证：CD=CB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•河源）如图，矩形OABC中，A（6，0），C（0，2
    		3
    ），D（0，3
    		3
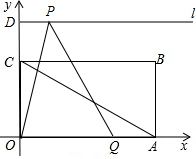    ），射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO=60°．
    （1）①点B的坐标是
    （6，2
    		3
    ）
    （6，2
    		3
    ）
    ；②∠CAO=
    30
    30
    度；③当点Q与点A重合时，点P的坐标为
    （3，3
    		3
    ）
    （3，3
    		3
    ）
    ；（直接填写答案）
    （2）设点P的横坐标为x，△OPQ与矩形OABC的重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．

    查看答案和解析>>

    同步练习册答案