
分析 先根据AD是BD上的中线求出BD的长,再根据勾股定理的逆定理判断出△ABD的形状,进而可得出∠ADC=90°,根据勾股定理即可求出AC的长,进而得出结论.
解答 解:△ABC是等腰三角形,
∵AD是BC边的中线,BC=16cm,
∴BD=DC=8cm,
∵AD2+BD2=152+82=172=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
在Rt△ADC中,
AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=17cm.
∴AC=AB,即△ABC是等腰三角形.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
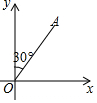 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com