
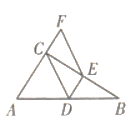
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB的中线,E为边BC的中点,连接DE,过点E作EF∥CD交AC的延长线于点F.若AB=13,BC=12,则四边形CDEF的周长为________。
科目:初中数学 来源: 题型:
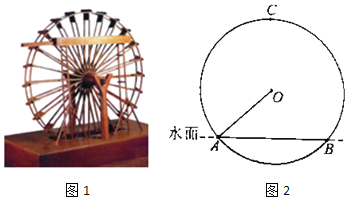
【题目】筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )

A. 34B. 32C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组为测量如图(①所示的一段古城墙的高度,设计用平面镜测量的示意图如图②所示,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处。

(1)已知AB⊥BD、CD⊥BD,且测得AB=1.2m,BP=1.8m.PD=12m,求该城墙的高度(平面镜的原度忽略不计):
(2)请你设计一个测量这段古城墙高度的方案。
要求:①面出示意图(不要求写画法);②写出方案,给出简要的计算过程:③给出的方案不能用到图②的方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
(1) 求证:DE⊥AC;
(2) 连结OC交DE于点F,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):
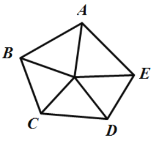
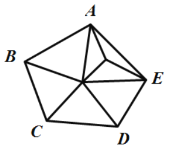
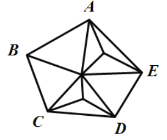
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com