
 x+3经过顶点B,与y轴交于顶点C,AB∥OC.
x+3经过顶点B,与y轴交于顶点C,AB∥OC.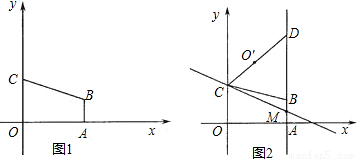
 x+3中得y=2,即可求出B点的坐标;
x+3中得y=2,即可求出B点的坐标; x过P,Q作x轴平行线,设P(x,-
x过P,Q作x轴平行线,设P(x,- x+3)∴Q(x-4,4-
x+3)∴Q(x-4,4- x)代入y=
x)代入y= x中得x=5∴P1(5,
x中得x=5∴P1(5, ),同理P2(-2,4),当BC为对角线时,设P(a,-
),同理P2(-2,4),当BC为对角线时,设P(a,- a+3)Q(b,
a+3)Q(b, b)
b)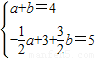
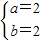 ,∴p3(2,2).
,∴p3(2,2). x+3中,得:y=2,
x+3中,得:y=2, x+3,当x=0时y=3,
x+3,当x=0时y=3,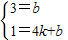 ,解得
,解得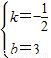 ,
,
 x+3,
x+3, x,
x, x+3),
x+3), x)代入y=
x)代入y= x中,得:x=5,
x中,得:x=5, ),
), a+3)、Q(b,
a+3)、Q(b, b)
b)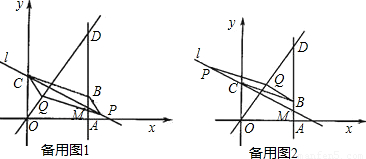
 ,
, ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
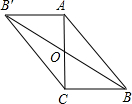 (2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( )
(2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( )查看答案和解析>>
科目:初中数学 来源: 题型:
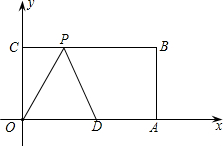 (2013•江西模拟)如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为( )
(2013•江西模拟)如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
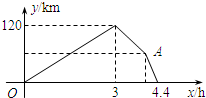 车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是
车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com