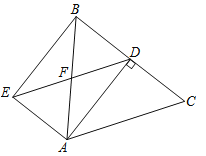
【题目】如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．求四边形AEBD的面积
科目：初中数学 来源： 题型：
【题目】（【材料阅读】阅读下列一段文字，然后回答下列问题．
已知平面内两点M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算：
MN=
．
例如：已知P（3，1）、Q（1，﹣2），则这两点间的距离PQ=
=
．
【直接应用】
（1）已知A（2，-3）、B（-4，5），试求A、B两点间的距离；
（2）已知△ABC的顶点坐标分别为A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC的形状吗？请说明理由．
【深度应用】
（3）如图，在平面直角坐标系xOy中，二次函数y=x2﹣4的图象与x轴相交于两点A、B，（点A在点B的左边）
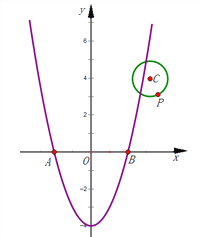
①求点A、B的坐标；
②设点P（m，n）是以点C（3，4）为圆心、1为半径的圆上一动点，求PA2+PB2的最大值；
查看答案和解析>>
科目：初中数学 来源： 题型：
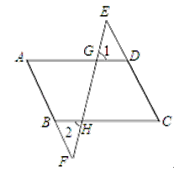
【题目】如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1＝∠2，∠A＝∠C，试说明AD∥BC和AB∥CD．
请完成下面的推理过程，并填空（理由或数学式）：
∵∠1＝∠2（ ）
∠1＝∠AGH（ ）
∴∠2＝∠AGH（ ）
∴AD∥BC（ ）
∴∠ADE＝∠C（ ）
∵∠A＝∠C（ ）
∴∠ADE＝∠A
∴AB∥CD（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
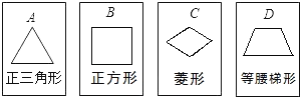
【题目】有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次模牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张牌面图形既是中心对称图形又是轴对称图形的纸牌的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分，则矩形的周长（ ）
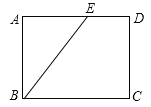
A. 16cm B. 22cm和16cm C. 26cm D. 22cm和26cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB∥CD，直线l与直线AB，CD相交于点E，F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处．
⑴若∠PEF＝48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 ．
⑵若∠PEF＝75°，∠CFQ＝
∠PFC，求∠EFP的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为
千米，出租车离甲地的距离为
千米，两车行驶的时间为x小时，、关于x的图象如图所示：
（1）根据图象，分别写出、关于x的关系式（需要写出自变量取值范围）；
（2）当两车相遇时，求x的值；
（3）甲、乙两地间有
、
两个加油站，相距200千米，若客车进入加油站时，出租车恰好进入加油站，求加油站离甲地的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知A（a，b），B（2，2），且|a-b+8|+
=0．
（1）求点A的坐标；
（2）过点A作AC⊥x轴于点C，连接BC，AB，延长AB交x轴于点D，设AB交y轴于点E，那么OD与OE是否相等？请说明理由．
（3）在x轴上是否存在点P，使S△OBP=S△BCD？若存在，请求出P点坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 观察下列等式：
第1个等式：a1＝
＝
×（
﹣
）；
第2个等式：a2＝
＝×（﹣
）；
第3个等式：a3＝
＝×（﹣
）；
第4个等式：a4＝
＝×（﹣
）；
…
请解答下列问题：
（1）按以上规律列出第5个等式：a5＝ ＝ ；
第n（n为正整数）个等式：an＝ ＝ ；
（2）求a1+a2+a3+a4+…+a2019的值；
（3）数学符号
＝f（1）+f（2）+f（3）+…+f（n），试求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
