
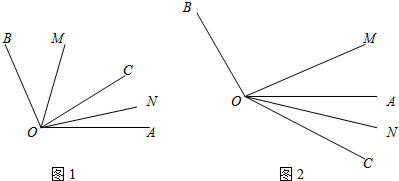
���� ��1�������ý�ƽ���ߵ����ʵõ���CON=$\frac{1}{2}$��AOC����COM=$\frac{1}{2}$��BOC�������á�MON=��COM+��CON���㣻
��2�����ݣ�1���Ľ��ۣ����ɽ��
��3�������ý�ƽ���ߵ����ʵõ���CON=$\frac{1}{2}$��AOC����COM=$\frac{1}{2}$��BOC�������á�MON=��COM-��CON���㣬���ɽ��
��� �⣺��1����OMƽ�֡�BOC��ONƽ�֡�AOC��
���CON=$\frac{1}{2}$��AOC����COM=$\frac{1}{2}$��BOC��
���ԡ�MON=��COM+��CON=$\frac{1}{2}$��BOC+$\frac{1}{2}$��AOC=$\frac{1}{2}$����BOC+��AOC��=$\frac{1}{2}��AOB$=50�㣻
��2�����ݣ�1���Ľ��ۿɵã�$��MON=\frac{1}{2}��$��
�ʴ�Ϊ��$��MON=\frac{1}{2}��$��
��3����OMƽ�֡�BOC��ONƽ�֡�AOC��
���CON=$\frac{1}{2}$��AOC����COM=$\frac{1}{2}$��BOC��
���ԡ�MON=��COM-��CON=$\frac{1}{2}$��BOC-$\frac{1}{2}$��AOC=$\frac{1}{2}$����BOC-��AOC��=$\frac{1}{2}��AOB$=$\frac{1}{2}$����
���� ���⿼���˽ǵļ��㣬�Լ���ƽ���ߣ��������Ĺؼ������ýǵĺ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
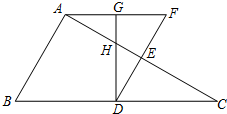 ��ͼ����ABC�У�BC=2AB����D��E�ֱ���BC��AC���е㣬����A��AF��BC���߶�DE���ӳ����ڵ�F��ȡAF���е�G������DG��GD��AE���ڵ�H��
��ͼ����ABC�У�BC=2AB����D��E�ֱ���BC��AC���е㣬����A��AF��BC���߶�DE���ӳ����ڵ�F��ȡAF���е�G������DG��GD��AE���ڵ�H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
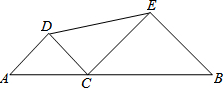 ��ͼ���߶�AB�ij�Ϊ10��CΪAB�ϵ�һ�����㣬�ֱ���AC��BCΪб����AB��ͬ������������ֱ�ǡ�ACD�͡�BCE����ôDE������Сֵ��5��
��ͼ���߶�AB�ij�Ϊ10��CΪAB�ϵ�һ�����㣬�ֱ���AC��BCΪб����AB��ͬ������������ֱ�ǡ�ACD�͡�BCE����ôDE������Сֵ��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
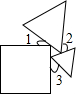 һ�������κ������ȱ������ε�λ����ͼ��ʾ������3=60�㣬���1+��2=��������
һ�������κ������ȱ������ε�λ����ͼ��ʾ������3=60�㣬���1+��2=��������| A�� | 180�� | B�� | 100�� | C�� | 90�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com