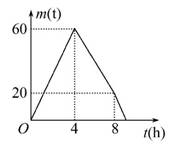
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(t)与时间t(h)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A.8.4h B.8.6h C.8.8h D.9h
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.
请解答下列问题:
(1)S1= .
(2)通过探究,用含n的式子表示Sn,则Sn= .
查看答案和解析>>
科目：初中数学 来源： 题型：
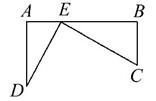
如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10
km,现在要在铁路AB附近建一个土特产收购站E,使得C,D两村到E站的距离相等,则E站应建在距A站多少千米处?
查看答案和解析>>
科目：初中数学 来源： 题型：
在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的
速度
前进.
(1)情境a,b所对应的函数图象分别是 , (填写序号).
(2)请你为剩下的函数图象写出一个适合的情境.
查看答案和解析>>
科目：初中数学 来源： 题型：
已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为( )
A.6 B.8 C.10 D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=25(t/h),所以剩余的20t完全调出需要20÷25=0.8(h).
A、
B、
C、
D、
A.90° B.60° C.45° D.30°
