【题目】如图所示，有一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，则这块地的面积． 
【答案】解：如图，连接AC．
在△ACD中，∵AD=4米，CD=3米，∠ADC=90°，
∴AC=5米，
又∵AC2+BC2=52+122=132=AB2，
∴△ABC是直角三角形，
∴这块地的面积=△ABC的面积﹣△ACD的面积= 
×5×12﹣ ×3×4=24（平方米）．
【解析】连接AC，先利用勾股定理求出AC，再根据勾股定理的逆定理判定△ABC是直角三角形，那么△ABC的面积减去△ACD的面积就是所求的面积．
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
导学全程练创优训练系列答案科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB． 
（1）求证：四边形PMAN是正方形；
（2）求证：EM=BN．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.
（1）如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射出去，若b镜反射出的光线n平行于m，且∠1=30
，则∠2= ，∠3= ；
（2）在（1）中，若∠1=70
，则∠3= ；若∠1=a，则∠3= ；
（3）由（1）（2）请你猜想：当∠3= 时，任何射到平面镜a上的光线m经过平面镜a和b的两次反射后，入射光线m与反射光线n总是平行的？请说明理由.
（提示：三角形的内角和等于180
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下是两张不同类型火车的车票（“
次”表示动车，“
次”表示高铁）：
（1）根据车票中的信息填空：该列动车和高铁是__________向而行（填“相”或“同”）．
（2）已知该列动车和高铁的平均速度分别为
、
，两列火车的长度不计．
①经过测算，如果两列火车直达终点（即中途都不停靠任何站点），高铁比动车将早到
，求
、
两地之间的距离．
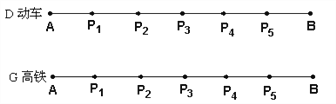
②在①中测算的数据基础上，已知
、
两地途中依次设有
个站点
、
、
、
、
，且
，动车每个站点都停靠，高铁只停靠
、
两个站点，两列火车在每个停靠站点都停留
．求该列高铁追上动车的时刻．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是菱形，对角线AC、BD相交于点O，分别延长OB，OD到点E，F，使BE=DF，顺次连接A、E、C、F各点． 
（1）求证：∠FAD=∠EAB．
（2）若∠ADC=130°，要使四边形AECF是正方形，求∠FAD的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
