
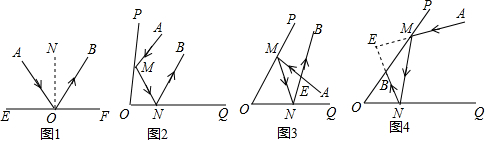
分析 (1)根据反射角等于入射角,可得∠AON=∠BON,根据NO⊥EF,即可得到∠AOE=∠BOF;根据反射角等于入射角,可得∠BON=$\frac{1}{2}$∠AOB=40°,再根据NO⊥EF,即可得出∠BOF的度数;
(2)(Ⅰ)设∠AMP=∠NMO=α,∠BNQ=∠MNO=β,根据∠AMN+∠BNM=180°,可得α+β=90°,再根据三角形内角和定理进行计算即可;
(Ⅱ)设∠AMP=∠NMO=α,∠BNQ=∠MNO=β,根据三角形内角和定理可得α+β=180°-∠O,再根据三角形内角和定理可得可得∠MEN=2(α+β)-180°,进而得出∠MEN+2∠O=180°;
(Ⅲ)设∠AMP=∠NMO=α,∠BNO=∠MNQ=β,根据三角形外角性质可得∠E=2(β-α),再根据三角形外角性质可得∠O=β-α,进而得出∠E=2∠O.
解答 解:(1)如图1,根据反射角等于入射角,可得∠AON=∠BON,
∵NO⊥EF,
∴∠AOE=∠BOF=65°;
根据反射角等于入射角,可得∠BON=$\frac{1}{2}$∠AOB=40°,
∵NO⊥EF,
∴∠BOF=90°-40°=50°;
故答案为:65,50;
(2)(Ⅰ)如图2,设∠AMP=∠NMO=α,∠BNQ=∠MNO=β,
当AM∥BN时,∠AMN+∠BNM=180°,
即180°-2α+180°-2β=180°,
∴180°=2(α+β),
∴α+β=90°,
∴△MON中,∠O=180°-∠NMO-∠MNO=180°-(α+β)=90°,
∴当∠POQ为90度时,光线AM∥NB;
(Ⅱ)如图3,设∠AMP=∠NMO=α,∠BNQ=∠MNO=β,
∵△MON中,∠O=180°-α-β,
∴α+β=180°-∠O,
∵∠EMN=180°-2α,∠ENM=180°-2β,
∴△MEN中,∠MEN=180°-∠EMN-∠ENM=180°-(180°-2α)-(180°-2β)=2(α+β)-180°,
∴∠MEN=2(180°-∠O)-180°=180°-2∠O,
即∠MEN+2∠O=180°;
(Ⅲ)如图4,设∠AMP=∠NMO=α,∠BNO=∠MNQ=β,
∴∠AMN=180°-2α,∠MNE=180°-2β,
∵∠AMN是△MEN的外角,
∴∠E=∠AMN-∠MNE=(180°-2α)-(180°-2β)=2(β-α),
∵∠MNQ是△MNO的外角,
∴∠O=∠MNQ-∠NMO=β-α,
∴∠E=2∠O.
故答案为:∠E=2∠O.
点评 本题考查了平行线的判定与性质,三角形外角的性质以及三角形内角和定理的综合应用,解题时注意:两直线平行,同旁内角互补;三角形的一个外角等于与它不相邻的两个内角的和.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
 相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.
相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,AB=BC,∠ABC=90°,以AB为直径作半圆O,P是BC边上一动点(不与B、c重合),过点P作半圆O的切线,与过A点的垂线交于点Q.AC与PQ,OQ分别交于点E,F,如果P,C,F三点构成的三角形与△AEO相似,那么∠CPF的度数是90°或60°.
在Rt△ABC中,AB=BC,∠ABC=90°,以AB为直径作半圆O,P是BC边上一动点(不与B、c重合),过点P作半圆O的切线,与过A点的垂线交于点Q.AC与PQ,OQ分别交于点E,F,如果P,C,F三点构成的三角形与△AEO相似,那么∠CPF的度数是90°或60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
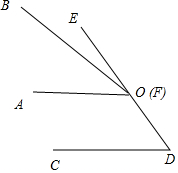 两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.
两个角∠BOA和∠EDC,∠AOB保持不动,∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com