练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．不等式：$\frac{x-2}{2}$＜$\frac{2-x}{3}$的解集是x＜2．

    分析 先去分母，再去括号，移项，合并同类项，最后系数化为1即可．

    解答 解：去分母，得3x-6＜4-2x，
    移项合并，得5x＜10，
    系数化为1，得x＜2．
    故答案是：x＜2．

    点评 本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意在不等式两边都除以一个负数时，应改变不等号的方向这一点而出错．解不等式要依据不等式的基本性质：
    ①在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；
    ②在不等式的两边同时乘以或除以同一个正数不等号的方向不变；
    ③在不等式的两边同时乘以或除以同一个负数不等号的方向改变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．下列说法不正确的是（　　）
    A．（-$\frac{1}{4}$）2的平方根是$±\frac{1}{4}$B．-5是25的一个平方根
    C．0.9的算术平方根是0.3D．$\root{3}{-27}$=-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

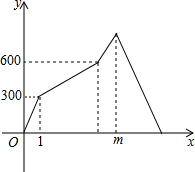    16．老王乘坐7：00的高铁从A地去B地开会，出发后发现一份重要的文件未带，让同事小李乘坐8：00的动车将文件送至B地．因火车会车原因，动车在途中停留了半小时．若高铁与动车的行驶路线相同、行驶过程中两车都以各自的速度匀速行驶，且A地到B地的全线长为1350千米．设高铁出发时间为t小时，高铁与动车的距离为y千米，y与t的函数图象如图所示．（注：高铁出发时，动车在A地；高铁到达B地后进行补给，直至动车到达B地．）
    （1）高铁速度为300km/h，m=4.5h．
    （2）求动车的速度．
    （3）若小李当天16：00前能到达B地火车站，老王的会议就不会受影响，请通过计算说明老王的会议会不会受影响．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列分式中，最简分式是（　　）
    A．$\frac{{3{x^2}}}{4xy}$B．$\frac{{{x^2}+{y^2}}}{x+y}$C．$\frac{x-2}{{{x^2}-4}}$D．$\frac{1+x}{{{x^2}+2x+1}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．计算：|-2|+20-（-1）2=（　　）
    A．2B．0C．1D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．
    问：牛、羊各直金几何？”
    译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、
    每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，可列方程组为（　　）
    A．$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$B．$\left\{\begin{array}{l}{5x+2y=8}\\{2x+5y=10}\end{array}\right.$
    C．$\left\{\begin{array}{l}{5x+2y=10}\\{x+5y=8}\end{array}\right.$D．$\left\{\begin{array}{l}{x+y=2}\\{2x+5y=8}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．为了降低塑料袋--“白色污染”对环境污染．学校组织了对使用购物袋的情况的调查，小明同学5月8日到站前市场对部分购物者进行了调查，据了解该市场按塑料购物袋的承重能力分别提供了0.1元，0.2元，0.3元三种质量不同的塑料袋，下面两幅图是这次调查得到的不完整的统计图（若每人每次只使用一个购物袋），请你根据图中的信息，回答下列问题：
    （1）这次调查的购物者总人数是120人；
    （2）请补全条形统计图，并说明扇形统计图中0.2元部分所对应的圆心角是99度，0.3元部分所对应的圆心角是36度；
    （3）若5月8日到该市场购物的人数有3000人次，则该市场应销售塑料购物袋多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．将样本容量为100的样本编制成组号①～⑧的八个组，简况如表所示：
    组号①②③④⑤⑥⑦⑧
    频数14111213■131210
    那么第⑤组的频率是（　　）
    A．14B．15C．0.14D．0.15

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在△ABC中，AB=6，AC=8，BC=10，D是△ABC内部或BC边上的一个动点（与B、C不重合），以D为顶点作△DEF，使△DEF∽△ABC（相似比k＞1），EF∥BC．
    （1）求∠D的度数；
    （2）若两三角形重叠部分的形状始终是四边形AGDH．
    ①如图1，连接GH、AD，当GH⊥AD时，请判断四边形AGDH的形状，并证明；
    ②当Ⅰ的面积最大时，过A作AP⊥EF于P，且AP=AD，求k的值．

    查看答案和解析>>

    同步练习册答案