
 如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号)
如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号) 分析 根据旋转的性质得到CM=CN,BM=AN,故①正确,②错误;△BCM≌△ACN,于是得到S△BCM=S△ACN,求得S四边形AMCN=S△ACM+S△ACN=S△ABC-S△ABM;故③正确;连接MN,根据等边三角形的性质得到∠ACB=60°,推出△CMN是等边三角形,根据等边三角形的性质得到∠CMN=60°,MN=CM=6,根据勾股定理的逆定理得到∠AMN=90°,求得∠AMC=150°,故④错误.
解答 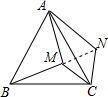 解:∵△BMC绕点C顺时针旋转得到△ANC,
解:∵△BMC绕点C顺时针旋转得到△ANC,
∴CM=CN,BM=AN,故①正确,②错误;
△BCM≌△ACN,
∴S△BCM=S△ACN,
∴S四边形AMCN=S△ACM+S△ACN=S△ABC-S△ABM;故③正确;
连接MN,∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACN=∠BCM,
∴∠MCN=60°,
∴△CMN是等边三角形,
∴∠CMN=60°,MN=CM=6,
在△AMN中,∵AM2+MN2=82+62=102=AN2,
∴∠AMN=90°,
∴∠AMC=150°,故④错误,
故答案为:①③.
点评 本题考查了全等三角形的性质,旋转的性质,等边三角形的性质,勾股定理的逆定理,连接MN构造等边三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 尺规作图:如图,已知线段a,b.
尺规作图:如图,已知线段a,b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠AOB=90°,点P为∠AOB内一点.
如图,∠AOB=90°,点P为∠AOB内一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长;
(1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com