
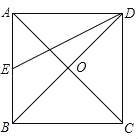
【题目】如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,那么EE1的长为______.
【答案】![]()
【解析】
根据正方形的性质得到AB=AD=4,根据勾股定理得到BD=![]() ,DE=
,DE=![]() ,过B作BF⊥DD1于F,根据相似三角形的性质得到EF=
,过B作BF⊥DD1于F,根据相似三角形的性质得到EF=![]() ,求得DF=
,求得DF=![]() ,根据旋转的性质得到BD1=BD,∠D1BD=∠E1BE,BE1=BE,根据相似三角形的性质即可得到结论.
,根据旋转的性质得到BD1=BD,∠D1BD=∠E1BE,BE1=BE,根据相似三角形的性质即可得到结论.
解:∵正方形ABCD的边长为4,
∴AB=AD=4,
∴BD=![]() AB=4
AB=4![]() ,
,
∵点E为边AB的中点,
∴AE=![]() AB=2,
AB=2,
∵∠EAD=90°,
∴DE=![]() ,
,
过B作BF⊥DD1于F,
∴∠DAE=∠EFB=90°,
∵∠AED=∠BFE,
∴△ADE∽△FEB,
![]()
![]()
∴EF=![]() ,
,
∴DF=![]() ,
,
∵△BED绕着点B旋转至△BD1E1,
∴BD1=BD,∠D1BD=∠E1BE,BE1=BE,
∴DD1=2DF=![]() ,△D1BD∽△E1BE,
,△D1BD∽△E1BE,
∴![]() ,
,
∴ ,
,
∴EE1=![]() ,
,
故答案为![]() .
.



 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的点
中的点![]()
![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比称为点
的比称为点![]() 的“湘一比”,记为
的“湘一比”,记为![]() ,如点
,如点![]() ,则
,则![]() .
.
(1)若![]() 在直线
在直线![]() 上,求点
上,求点![]() 的“湘一比”
的“湘一比”![]() 及直线
及直线![]() 与
与![]() 轴夹角的正切值;
轴夹角的正切值;
(2)已知点![]() 的“湘一比”
的“湘一比”![]() 为
为![]() ,且
,且![]() 在
在![]() 上,
上,![]() 的半径为
的半径为![]() ,若点
,若点![]() 在
在![]() 上,求
上,求![]() 的“湘一比”
的“湘一比”![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 为正整数,且
为正整数,且![]() ,对一切实数
,对一切实数![]() ,如果直线
,如果直线![]() 与二次函数
与二次函数![]() 交于
交于![]() 、
、![]() ,且
,且![]() ,求点
,求点![]() 的“湘一比”
的“湘一比”![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
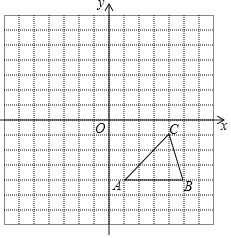
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O对称的△A2B2C2;
(3)△A1B1C1与△A2B2C2关于某个点对称,则这个点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
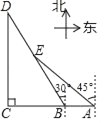
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
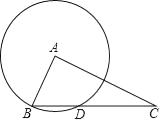
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
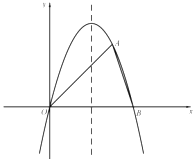
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于原点
轴交于原点![]() 和点
和点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)求![]() 的值;
的值;
(3)点![]() 在抛物线的对称轴上,如果
在抛物线的对称轴上,如果![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图).
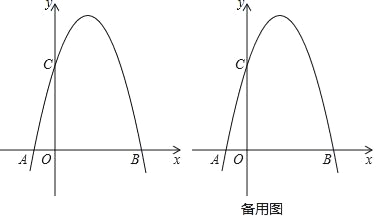
(1)求平移后的抛物线的表达式;
(2)如果点D在线段CB上,且CD=![]() ,求∠CAD的正弦值;
,求∠CAD的正弦值;
(3)点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com