
����Ŀ����֪������AOB�У�Բ�Ľǡ�AOB��120�����뾶OA��OB��8��
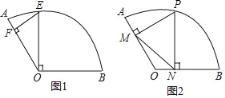
��1����ͼ1������O��OE��OB������AB�ڵ�E���ٹ���E��EF��OA�ڵ�F����FO�ij�����FEO�Ķ�����
��2����ͼ2�����PΪ��AB�ϵĶ��㣬����P��PM��OA�ڵ�M��PN��OB�ڵ�N����M��N�ֱ��ڰ뾶OA��OB�ϣ�����MN����
�����P�˶���·�����Ƕ��٣�
��MN�ij����Ƿ��Ƕ�ֵ������ǣ�����������ֵ�������ǣ���˵�����ɣ�
��3���ڣ�2���е������£�����D����PMN�����ģ�ֱ��д����D�˶���·������
���𰸡���1��OF��4![]() ����FEO��60������2���ٵ�P�˶���·����Ϊ
����FEO��60������2���ٵ�P�˶���·����Ϊ![]() ����MN��4
����MN��4![]() ���Ƕ�ֵ����3����D�˶���·����Ϊ
���Ƕ�ֵ����3����D�˶���·����Ϊ![]() ��
��
��������
��1���������AOE�����ɵó����ۣ�
��2���ٵ���M���O�غ�ʱ����PMB��30��������N���O�غ�ʱ����PNA��30�������������P�˶�·�����Ե�Բ�Ľ���120����30����30����60��������û�����ʽ���ɵó����ۣ�
�����жϳ���P��M��O��N�ĵ����ͬһ��Բ������H�ϣ��������MK��2![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��3�����жϳ�������PMN�����Բ��Բ�ĵ��˶��켣�������ݻ�����ʽ���ɵó����ۣ�
��1����OE��OB��
���BOE��90����
�ߡ�AOB��120����
���AOE��30����
��EF��OA��
���EFO��90����
��Rt��EFO��OE��OB��8��
��OF��OEcos30����4![]() ����FEO��90����30����60����
����FEO��90����30����60����
�ʴ�Ϊ��4![]() ��60��
��60��
��2���ٵ�P�ڻ�AB���˶�����·��Ҳ��һ�λ����������֪��
����M���O�غ�ʱ����PMB��30����
����N���O�غ�ʱ����PNA��30����
���P�˶�·�����Ե�Բ�Ľ���120����30����30����60����
���P�˶���·������![]() ��
��
���Ƕ�ֵ��
��ͼ1������PO��ȡPO���е�H������MH��NH��
����Rt��PMO��Rt��PNO�У���H��б��PO���е㣬
��MH��NH��PH��OH��![]() PO��4��
PO��4��
�����Բ�Ķ����֪����P��M��O��N�ĵ����ͬһ��Բ������H�ϣ�
�֡ߡ�MON��120������PMO����PNO��90����
���MPN��60������MHN��2��MPN��120����
����H��HK��MN��������K��
�ɴ��������ã�MK��KN��![]() MN��
MN��
����Rt��HMK����MHK��60����MH��4����MK��2![]() ��
��
��MN��2MK��4![]() ���Ƕ�ֵ��
���Ƕ�ֵ��
��3���ɣ�2��֪����P��M��O��N�ĵ㹲Բ��
��H����PMN�����Բ��Բ�ģ�
������H�͵�D�غϣ�
��OD��PD��
���D���Ե�OΪԲ��![]() OP��4Ϊ�뾶��
OP��4Ϊ�뾶��
�ߵ�P�˶�·�����Ե�Բ�Ľ���120����30����30����60����
���D�˶�·�����Ե�Բ�Ľ���120����30����30����60����
���D�˶���·����Ϊ![]() ��
��


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
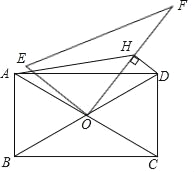
����Ŀ����ͼ���ھ���ABCD�У�AB��4��BC��4![]() ���Խ���AC��BD�ཻ�ڵ�O���ֽ�һ��ֱ�����ǰ�OEF��ֱ�Ƕ�����O�غϣ�������O��ת�����ǰ壬������D��DH��OF�ڵ�H������AH����ת���Ĺ����У�AH����СֵΪ_____��
���Խ���AC��BD�ཻ�ڵ�O���ֽ�һ��ֱ�����ǰ�OEF��ֱ�Ƕ�����O�غϣ�������O��ת�����ǰ壬������D��DH��OF�ڵ�H������AH����ת���Ĺ����У�AH����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
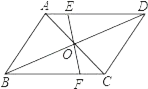
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD����O��EF����O��AD��BC�ֱ���E��F����AB��4��BC��5��OE��1.5�����ı���EFCD���ܳ�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ϰ�ȥͼ�������г�����ij��ͼ�飬��һ����1200Ԫ�������ɱ����������鶨��7Ԫ���ۣ��ܿ����꣮���ڸ��鳩�����ڶ��ι���ʱ��ÿ������������ѱȵ�һ�������20%������1500Ԫ��������������ȵ�һ�ζ�10�������������۳�200��ʱ���������������Զ��۵�4������ʣ����飮
��1����һ�ι���Ľ����Ƕ���Ԫ��
��2�����ʸ��ϰ���������������������Ǯ�ˣ�����Ǯ�ˣ��������������أ�������Ǯ������٣���Ǯ�����٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
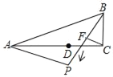
����Ŀ����ͼ����Rt��ABC�У���ACB��90����BC��2��AC��6����AC��ȡһ��D��ʹAD��4�����߶�AD�Ƶ�A��˳ʱ�뷽����ת����D�Ķ�Ӧ���ǵ�P������BP��ȡBP���е�F������CF������P��ת��CA���ӳ�����ʱ��CF�ij���_____������ת�����У�CF�������_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
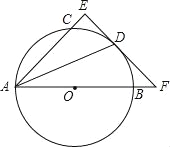
����Ŀ����ͼ��AB��ԲO��ֱ������C��D��ԲO�ϣ���ADƽ�֡�CAB������D��AC�Ĵ��ߣ���AC���ӳ����ཻ��E����AB���ӳ����ཻ�ڵ�F��
��֤��EF��ԲO���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ĩҪ������������ֲ�����棬�ӵ�ͼ�ϲ���·�߷��֣�������·����Ҫ����һ�Σ��ڳ���վ���ѡ��յ���A���յ���B����ͨ��a������վ���ѡ��յ���C����ͨ��b����ͨ��c���Ҿ���ͬһվ�㻻�ˣ��յ���Ͷ��2Ԫ����ͨ��Ͷ��1Ԫ��
��1����С���ڳ���վ������յ����ĸ��ʣ�
��2����С������ֲ��ǡ�û���3Ԫ�����ѵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
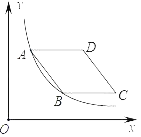
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ڵ�һ�����ڣ���BC��x��ƽ�У�A��B�����������ֱ�Ϊ3��1��������������ͼ��y��![]() ����A��B���㣬����ABCD�����Ϊ4
����A��B���㣬����ABCD�����Ϊ4![]() ����k��ֵΪ��������
����k��ֵΪ��������
A. 3B. 2![]() C. 2
C. 2![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����г�����ij���������³����������������ǰϦ������һ��Ʒ�����ӣ�ÿ�н�����40Ԫ�����й涨ÿ���ۼ۲�������45Ԫ�������������۾��鷢�֣����ۼ۶�Ϊÿ��45Ԫʱ��ÿ���������700�У�ÿ���ۼ�ÿ���1Ԫ��ÿ��Ҫ������20�У�
��1�������ÿ���������y���У���ÿ���ۼ�x��Ԫ��֮��ĺ�����ϵʽ��
��2����ÿ���ۼ۶�Ϊ����Ԫʱ��ÿ�����۵�����P��Ԫ�������������Ƕ��٣�
��3��Ϊ�ȶ���ۣ��йع������������������ӵ�ÿ���ۼ۲��ø���58Ԫ�����������Ҫÿ���ò�����6000Ԫ��������ô����ÿ�������������Ӷ��ٺУ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com