
分析 从锐角三角形和钝角三角形两种情况,利用三角形内角和定理先求出它的底角的度数,再求出腰上的高与底边的夹角的度数.
解答 解:在三角形ABC中,设AB=AC,BD⊥AC于D,∠ABD=40°.
①若是锐角三角形,∠A=90°-50°=40°,
∠ABC=∠C=(180°-40°)÷2=70°,
∠DBC=∠ABC-∠ABD=20°;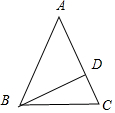
②若三角形是钝角三角形,∠BAC=50°+90°=140°,
此时∠ABC=∠C=(180°-140°)÷2=20°,
∠DBC=∠ABC+∠ABD=70°.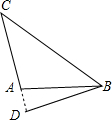
所以腰上的高与底边的夹角的度数是70°或20°.
故答案为20°或70°.
点评 此题主要考查学生对等腰三角形的性质和三角形内角和定理的理解和应用,此题的关键是熟练掌握三角形内角和定理.


科目:初中数学 来源: 题型:解答题
| 年份 | 第1年年底 | 第2年年底 | 第3年年底 | 第4年年底 |
| 绿化覆盖率﹙%﹚ | 22.2 | 23.8 | 25.4 | 27.0 |
| 年份 | 第5年年底 | … | 第10年年底 | |
| 绿化覆盖率﹙%﹚ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
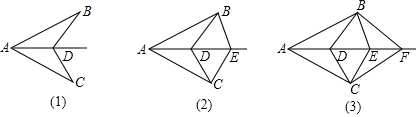
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 总体是1000筐苹果 | B. | 样本是50筐苹果 | ||
| C. | 总体是指1000筐苹果的等次 | D. | 样本是指苹果的等次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
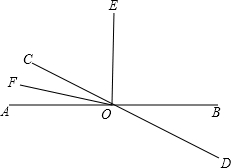 如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求:
如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com