
【题目】如图,抛物线经过A(![]() ,0),B(
,0),B(![]() ,0),C(0,2)三点.
,0),C(0,2)三点.
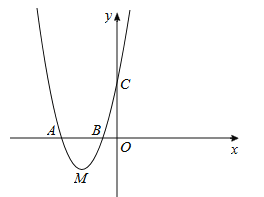
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)D(-1,-1);(3)(
;(2)D(-1,-1);(3)(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得抛物线的解析式;
(2)根据图形的割补法,可得面积的和差,根据二次函数的性质,可得答案;
(3)根据余角的性质,可得∠AMN=∠NKM,根据相似三角形的判定与性质,可得![]() ,根据解方程组,可得H点坐标.
,根据解方程组,可得H点坐标.
试题解析:(1)设抛物线的解析式为![]() ,将A(﹣2,0),B(
,将A(﹣2,0),B(![]() ,0)代入解析式,得:
,0)代入解析式,得: ,解得:
,解得:![]() .∴抛物线的解析式是
.∴抛物线的解析式是![]() ;
;
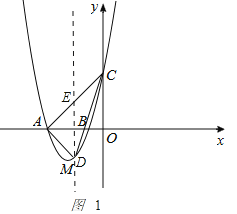
(2)由题意可求得AC的解析式为![]() ,如图1,设D点的坐标为(t,
,如图1,设D点的坐标为(t,![]() ),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=
),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=![]()
![]() ,用h表示点C到线段DE所在直线的距离,
,用h表示点C到线段DE所在直线的距离,
![]() =
=![]() ,∵﹣2<t<0,
,∵﹣2<t<0,
∴当t=﹣1时,△DCA的面积最大,此时D点的坐标为(﹣1,﹣1);
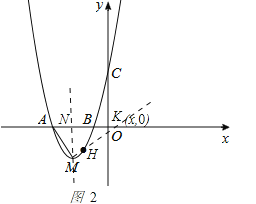
(3)存在点H满足∠AMH=90°,由(1)知M点的坐标为(![]() ,
,![]() ),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴
),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴![]() ,∴
,∴![]() =ANNK,∴
=ANNK,∴![]() ,解得
,解得![]() ,∴K点坐标为(
,∴K点坐标为(![]() ,0),∴直线MK的解析式为
,0),∴直线MK的解析式为![]() ,∴
,∴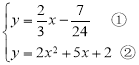 ,把①代入②,化简得
,把①代入②,化简得![]() .△=
.△=![]() ﹣4×48×55=64×4=256>0,∴
﹣4×48×55=64×4=256>0,∴![]() ,
,![]() ,将
,将![]() 代入
代入![]() ,解得
,解得![]() ,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(
,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(![]() ,
,![]() ).
).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() 、
、![]() 两种品牌的洗衣机,进价及售价如下表:
两种品牌的洗衣机,进价及售价如下表:
品牌 |
|
|
进价(元/台) | 1500 | 1800 |
售价(元/台) | 1800 | 2200 |
(1)该商场9月份用45000元购进![]() 、
、![]() 两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进
两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进![]() 、
、![]() 两种洗衣机的数量;
两种洗衣机的数量;
(2)该商场10月份又购进![]() 、
、![]() 两种品牌的洗衣机共用去36000元
两种品牌的洗衣机共用去36000元
①问该商场共有几种进货方案?请你把所有方案列出来;
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,点M,N分别表示数m,n则点M,N之间的距离为|m﹣n|.已知点A,B,C,D在数轴上分别表示数a,b,c,d,且|a﹣c|=|b﹣c|=![]() |d﹣a|=1(a≠b),则线段BD的长度为_____.
|d﹣a|=1(a≠b),则线段BD的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A.B对应的数分别为﹣2和7,点M为数轴上一动点.
(1)请画出数轴,并在数轴上标出点A、点B;
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是(A,B)的好点.
①若点M运动到原点O时,此时点M (A,B)的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是(B,A)的好点时,求点M的运动方向和运动时间
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆外,AC,BC与半圆交于D点和E点.
(1)请只用无刻度的直尺作出△ABC的两条高线,并写出作法;
(2)若AC=AB,连接DE,BE,求证:DE=BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com