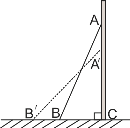
【题目】如图，一架2.5米长的梯子AB 斜靠在一座建筑物上，梯子底部与建筑物距离BC 为0.7米.
（1）求梯子上端A到建筑物的底端C的距离（即AC的长）；
（2）如果梯子的顶端A沿建筑物的墙下滑0.4米（即AA′=0.4米），则梯脚B将外移（即BB′的长）多少米？
【答案】（1）梯子上端A到建筑物的底端C的距离为2.4米；（2）梯脚B将外移0.8米.
【解析】
（1）在Rt△ABC中利用勾股定理求出AC的长即可；
（2）由（1）可以得出梯子的初始高度，下滑0.4米后，可得出梯子的顶端距离地面的高度，再次使用勾股定理，已知梯子的底端距离墙的距离为0.7米，可以得出，梯子底端水平方向上滑行的距离．
（1）在△ABC中，∠ACB=90°，AB=2.5,BC=0.7
根据勾股定理可知AC=
米
答：梯子上端A到建筑物的底端C的距离为2.4米.
（2）在△AˊBˊC中，∠ACB=90°，AˊBˊ=AB=2.5米, AˊC=AC-AAˊ=2.4-0.4=2米
根据勾股定理可知BˊC=
米
米
答：梯脚B将外移0.8米.
轻松课堂单元期中期末专题冲刺100分系列答案科目：初中数学 来源： 题型：
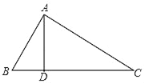
【题目】题目：如图，在△ABC中，点D是BC边上一点，连结AD，若AB＝10，AC＝17，BD＝6，AD＝8，解答下列问题：
（1）求∠ADB的度数；
（2）求BC的长．
小强做第（1）题的步骤如下：∵AB2＝BD2+AD2
∴△ABD是直角三角形，∠ADB＝90°．
（1）小强解答第（1）题的过程是否完整，如果不完整，请写出第（1）题完整的解答过程
（2）完成第（2）题．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
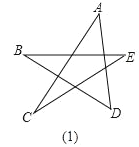
（1）请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；
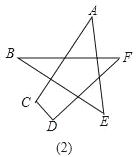
（2）若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；
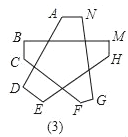
（3）若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于m的方程
（m-16）=7的解也是关于x的方程2（x-3）-n=52的解．
（1）求m，n的值；
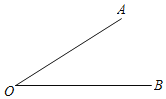
（2）已知∠AOB=m°，在平面内画一条射线OP，恰好使得∠AOP=n∠BOP，求∠BOP．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：(1)∣—6∣+(
—3.14)0—(
)-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
(3)
(4)(a-2b)(a+b)－3a(a+b)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某电器超市销售每台进价分别为200元，170元的A，B两种型号的电风扇，表中是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变，利润＝销售收入－进货成本)
(1)求A，B两种型号的电风扇的销售单价．
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，则A种型号的电风扇最多能采购多少台？
(3)在(2)的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列情境①④分别可以用哪幅图来近似地刻画?正确的顺序是（ ）
①一杯越来越凉的水(水温与时间的关系)；②一面冉冉升起的旗子(高度与时间的关系)；③足球守门员大脚开出去的球(高度与时间的关系)；④匀速行驶的汽车(速度与时间的关系).
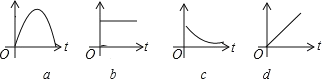
A. cdabB. acbdC. dabcD. cbad
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
