
【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

【答案】(1)见解析 (2)45![]() (3)
(3)![]() ;
;![]()
【解析】
(1)①根据A点横坐标及纵坐标的意义解答即可;
②根据函数图象可知,小明出发2小时,爸爸第一次到达度假村,此时小明离家40km,则离度假村的距离可求;
(2)求出小明及小明爸爸的速度,根据题意列方程求出爸爸在返回家的途中与小明相遇时的时间即可解决问题;
(3)由函数图象可知,小明爸爸在返回家的途中与小明相遇之前,不存在相距24km的情况,然后分![]() <t≤3和3<t≤4两种情况,分别列方程求解即可.
<t≤3和3<t≤4两种情况,分别列方程求解即可.
解:(1) ①图中点A表示:爸爸追上小明时,小明出发了![]() 小时,此时离家的距离为30km;
小时,此时离家的距离为30km;
②当爸爸第一次到达度假村后,小明离家40km,则离度假村的距离是20km;
(2)由函数图象可得:小明速度为:60![]() 20km/h,小明爸爸速度为:60
20km/h,小明爸爸速度为:60![]() 1=60km/h,
1=60km/h,
设爸爸在返回家的途中与小明相遇时的时间为t,
由题意得:20t+60(t-1)=60×2,
解得:t=![]() ,
,
20![]() =45km,
=45km,
故爸爸在返回家的途中与小明相遇时,小明离家的距离是45km;
(3)由函数图象可知,小明爸爸在返回家的途中与小明相遇之前,不存在相距24km的情况,
∴当![]() <t≤3时,
<t≤3时,
由题意得:20t-[60×2-60(t-1)]=24,
解得:![]() ,
,
当3<t≤4时,
由题意得:60×3-60(t-1)=24,
解得:![]() ,
,
答:当t的值为![]() 或
或![]() 时,小明与爸爸相距24km.
时,小明与爸爸相距24km.


科目:初中数学 来源: 题型:
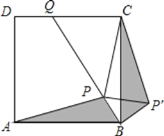
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() 的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=
的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE= ![]() ,OE=
,OE= ![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.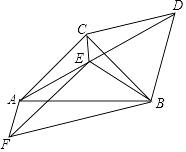
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )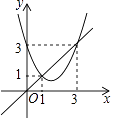
A.当1<x<3时,x2+(b﹣1)x+c<0
B.b+c=1
C.3b+c=6
D.b2﹣4c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为![]() ,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动
,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动![]() 设运动时间为t秒
设运动时间为t秒![]() .
.
![]() ,B两点间的距离等于______,线段AB的中点表示的数为______;
,B两点间的距离等于______,线段AB的中点表示的数为______;
![]() 用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
![]() 求当t为何值时,
求当t为何值时,![]() ?
?
![]() 若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农业观光园将一块面积为![]() 的观光园分成
的观光园分成![]() 三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲
三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 区域的面积是
区域的面积是![]() 的
的![]() 倍,记A区域的面积为
倍,记A区域的面积为![]() 区域的面积为
区域的面积为![]() .
.
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
|
| |
株/ |
|
|
|
数量 |
|
(1)完成上表(结果用含![]() 的代数式表示).
的代数式表示).
(2)若三种花卉共栽种![]() 株
株
①求![]() 与
与![]() 的值.
的值.
②若三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,求种植面积最大的花卉总价.
元,求种植面积最大的花卉总价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家研究发现,声音在空气中传播的速度y(米/秒)与气温x(°C)有关,当气温是0°C时,音速是331米/秒;当气温是5°C时,音速是334米/秒;当气温是10°C时,音速是337米/秒;气温是15°C时,音速是340米/秒;气温是20℃时,音速是343米/秒;气温是25°C时,音速是346米/秒;气温是30°C时,音速是349米/秒.
(1)请你用表格表示气温与音速之间的关系;
(2)表格反映了哪两个变量之间的关系?哪个是自变量?哪一个是对应的值?
(3)当气温是35°C时,估计音速y可能是多少?
(4)能否用一个式子来表示两个变量之间的关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com