
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌЙ§ЕуAзїжБЯпDEЃЌЧвТњзуBDЁЭDEгкЕуDЃЌCEЁЭDEгкЕуEЃЌЕБBЃЌCдкжБЯпDEЕФЭЌВрЪБЃЌ
ЃЈ1ЃЉЧѓжЄЃКDE=BD+CEЃЛ
ЃЈ2ЃЉШчЙћЩЯУцЬѕМўВЛБфЃЌЕБBЃЌCдкжБЯпDEЕФвьВрЪБЃЌШчЭМ2ЃЌЮЪBDЁЂDEЁЂCEжЎМфЕФЪ§СПЙиЯЕШчКЮЃПаДГіНсТлВЂжЄУї
ЃЈ3ЃЉШчЙћЩЯУцЬѕМўВЛБфЃЌЕБBЃЌCдкжБЯпDEЕФвьВрЪБЃЌШчЭМ3ЃЌЮЪBDЁЂDEЁЂCEжЎМфЕФЪ§СПЙиЯЕШчКЮЃПаДГіНсТлВЂжЄУїЃЎ

ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉBD=DE+CEЃЌМћНтЮіЃЛЃЈ3ЃЉDE=CE-BDЃЌМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬѕМўПЩвдЕУГіЁЯD=ЁЯE=90ЁуЃЌЁЯCAE=ЁЯABDЃЌОЭПЩвджЄУїЁїADBЁеЁїCEAОЭПЩвдЕУГіBD=AEЃЌAD=CEЃЌгЩDE=AD+AEОЭПЩвдЕУГіНсТлЃЛ
ЃЈ2ЃЉЭЌРэЕУЁїADBЁеЁїCEAЃЌОЭПЩвдЕУГіBD=AEЃЌAD=CEЃЌгЩAE=AD+DEОЭПЩвдЕУГіBD=CE+DEЃЛ
ЃЈ3ЃЉЭЌРэЕУЁїABDЁеЁїCAEЃЈAASЃЉЃЌОЭПЩвдЕУЃКAD=CEЃЌBD=AEЃЌгЩDE=AD-AEЃЌПЩЕУНсТлЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1ЃЌЁпBDЁЭDEЃЌCEЁЭDEЃЌ
ЁрЁЯD=ЁЯE=90ЁуЃЌ
ЁпЁЯBAC=90ЁуЃЌ
ЁрЁЯBAD+ЁЯCAE=90ЁуЃЎ
ЁпЁЯBAD+ЁЯABD=90ЁуЃЌ
ЁрЁЯCAE=ЁЯABDЃЎ
дкЁїADBКЭЁїCEAжаЃЌ

ЁрЁїADBЁеЁїCEAЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁпDE=AD+AEЃЌ
ЁрDE=CE+BDЃЛ
ЃЈ2ЃЉНтЃКBD=DE+CEЃЌ
РэгЩЃКШчЭМ2ЃЌ
ЁпBDЁЭDEЃЌCEЁЭDEЃЌ
ЁрЁЯADB=ЁЯCEA=90ЁуЃЎ
ЁрЁЯBAD+ЁЯABD=90ЁуЃЎ
ЁпЁЯBAD+ЁЯEAC=90Ёу
ЁрЁЯABD=ЁЯEACЃЎ
дкЁїADBКЭЁїCEAжаЃЌ

ЁрBD=AEЃЌAD=CEЃЎ
ЁпAE=AD+EDЃЌ
ЁрBD=DE+CEЃЎ
ЃЈ3ЃЉНтЃКDE=CE-BDЃЌ
РэгЩЪЧЃКШчЭМ3ЃЌЭЌРэвзжЄЕУЃКЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁпDE=AD-AEЃЌ
ЁрDE=CE-BDЃЎ


 КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ
КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ ЦкФЉН№ХЦОэЯЕСаД№АИ
ЦкФЉН№ХЦОэЯЕСаД№АИ ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ
ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФЖЅЕузјБъЗжБ№ЮЊAЃЈ1ЃЌ3ЃЉЁЂBЃЈ4ЃЌ2ЃЉЁЂCЃЈ2ЃЌ1ЃЉЃЎ

(1)зїГігыЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1ЃЌ ВЂаДГіA1ЁЂB1ЁЂC1ЕФзјБъЃЛ
(2)вддЕуOЮЊЮЛЫЦжааФЃЌдкдЕуЕФСэвЛВрЛГіЁїA2B2C2ЃЌ ЪЙ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРіЮЊСЫВтЦьИЫABЕФИпЖШЃЌаЁРіблОІОрЕиЭМ1.5УзЃЌаЁРіеОдкCЕуЃЌВтГіЦьИЫAЕФбіНЧЮЊ30oЃЌаЁРіЯђЧАзпСЫ10УзЕНДяЕуEЃЌДЫЪБЕФбіНЧЮЊ60oЃЌЧѓЦьИЫЕФИпЖШЁЃ
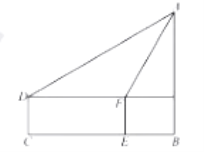
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌCFЁЭABгкFЃЌBEЁЭACгкEЃЌMЮЊBCЕФжаЕуЃЌBC=10ЃЎ
(1)ШєЁЯABC=50ЁуЃЌЁЯACB=60ЁуЃЌЧѓЁЯEMFЕФЖШЪ§ЃЛ
(2)ШєEF=4ЃЌЧѓЁїMEFЕФУцЛ§ЃЎ
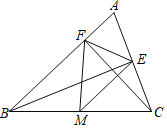
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЃЌ
ЃЌ![]() жЎМфгавЛЬѕЧњЯпКЭвЛЬѕЯпЖЮЃЌ
жЎМфгавЛЬѕЧњЯпКЭвЛЬѕЯпЖЮЃЌ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌМКжЊ
ЩЯЃЌМКжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌЙ§Еу
ЩЯвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() НЛЧњЯпгкЕу
НЛЧњЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎЩш
ЃЎЩш![]() ЃЌ
ЃЌ![]() СНЕуМфЕФОрРыЮЊ
СНЕуМфЕФОрРыЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() СНЕуМфЕФОрРыЮЊ
СНЕуМфЕФОрРыЮЊ![]() ЃЎЃЈЕБЕу
ЃЎЃЈЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() ЃЉаЁЫМИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§
ЃЉаЁЫМИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЫцздБфСП
ЫцздБфСП![]() ЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЫМЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ![]() ЃЉЭЈЙ§ШЁЕуЃЌЛЭМЃЌВтСПЃЌЕУЕНСЫ
ЃЉЭЈЙ§ШЁЕуЃЌЛЭМЃЌВтСПЃЌЕУЕНСЫ![]() гы
гы![]() ЕФМИзщжЕЃЌВЙШЋЯТБэЃК
ЕФМИзщжЕЃЌВЙШЋЯТБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЃЈЫЕУїЃКВЙШЋБэИёЪБЯрЙиЪ§жЕБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ![]() ЃЉдкЯТСаЦНУцжБНЧзјБъЯЕжаУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
ЃЉдкЯТСаЦНУцжБНЧзјБъЯЕжаУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЎ

ЃЈ![]() ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБ
ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФГЄЖШдМЮЊ__________
ЕФГЄЖШдМЮЊ__________![]() ЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉЃЎ
ЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЯТСаЬѕМўВЛФмХаЖЈетИіЫФБпаЮЪЧЦНааЫФБпаЮЕФЪЧ

AЃЎABЁЮDCЃЌADЁЮBCЁЁЁЁBЃЎAB=DCЃЌAD=BC
CЃЎAO=COЃЌBO=DOЁЁ ЁЁDЃЎABЁЮDCЃЌAD=BC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ6ЃЌЕуEЪЧБпABЩЯвЛЕуЃЌЕуPЪЧЖдНЧЯпBDЩЯвЛЕуЃЌЧвPEЁЭPCЃЎ
ЂХ ЧѓжЄЃКPCЃНPEЃЛ
ЂЦ ШєBEЃН2ЃЌЧѓPBЕФГЄ.
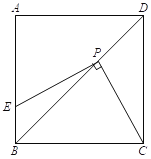
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
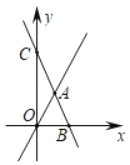
ЁОЬтФПЁПвбжЊжБЯпl1ЃКyЃНkxЙ§ЕуЃЈ1ЃЌ2ЃЉЃЌгыжБЯпl2ЃКyЃНЉ3x+bЯрНЛгкЕуAЃЌШєl2гыxжсНЛгкЕуBЃЈ2ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГіжБЯп11ЃЌl2ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїOACЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌAB=3ЃЌAC=4ЃЌBC=5ЃЌP ЮЊБп BC ЩЯвЛЖЏЕуЃЌPEЁЭAB гк EЃЌPFЁЭACгк FЃЌM ЮЊ EF жаЕуЃЌдђ AM ЕФзюаЁжЕЮЊЃЈ ЃЉ
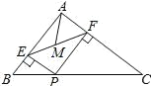
A.1B.1.3C.1.2D.1.5
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com