
【题目】已知△ABC中,∠BAC=100°.
(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;
(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;
(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)∠BOC=180°-
;(3)∠BOC=180°-![]() ,八等分线.
,八等分线.
【解析】
根据三角形内角和定理先求得∠ABC+∠ACB的度数,
(1)根据角平分线的定义可求得∠OBC+∠OCB的度数,从而利用三角形内角和定理求∠BOC的度数;
(2)根据三等分线的定义可求得∠OBC+∠OCB的度数,从而利用三角形内角和定理求∠BOC的度数;
(3)根据n等分线的定义可表示出∠OBC+∠OCB的度数,从而利用三角形内角和定理表示出∠BOC的度数,然后将∠BOC=170°代入求出n的值即可.
解:∵∠BAC=100°,
∴∠ABC+∠ACB=180°-100°=80°,
(1)∵点O是∠ABC和∠ACB的角平分线的交点,
∴∠OBC+∠OCB=![]() ∠ABC +
∠ABC +![]() ∠ACB =
∠ACB =![]() (∠ABC+∠ACB)=40°,
(∠ABC+∠ACB)=40°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-40°=140°;
(2)∵点O是∠ABC和∠ACB的三等分线的交点,
∴∠OBC+∠OCB=![]() ∠ABC +
∠ABC +![]() ∠ACB =
∠ACB =![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ,
,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-![]() =
=![]() ;
;
(3)∵点O是∠ABC和∠ACB的n等分线的交点,
∴∠OBC+∠OCB=![]() ∠ABC +
∠ABC +![]() ∠ACB =
∠ACB =![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ,
,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-![]() ,
,
当∠BOC=170°时,即170°=180°-![]() ,
,
解得:n=8,即是八等分线的交线所成的角.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
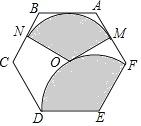
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元 ![]() 度;
度;
(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、A、F三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
己知:______________________________________________________.
求证:______________________________________________________.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的![]() 的圆心A在抛物线y=(x-3)2-1上,AB//x轴交
的圆心A在抛物线y=(x-3)2-1上,AB//x轴交 ![]() 于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )
于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )

A. y=(x-4)2-1 B. y=(x-3)2 C. y=(x-2)2-1 D. y=(x-3)2-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,……如此继续运动下去.设Pn(xn,yn),n=1、2、3、……,则x1+x2+……+x2014+x2015的值为( )

A. 1 B. 3 C. -1 D. 2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得![]() .
.
(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com