
【题目】如图,△ABC中,AB=AC=2![]() ,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
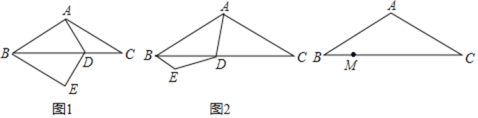
(1)如图1,若AD=DC,则BE的长为 ,BE2+CD2与AD2的数量关系为 ;
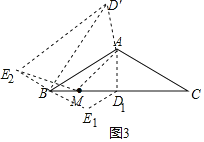
(2)如图2,点D为BC边山任意一点,线段BE、CD、AD是否依然满足(1)中的关系,试证明;
(3)M为线段BC上的点,BM=1,经过B、E、D三点的圆最小时,记D点为D1,当D点从D1处运动到M处时,E点经过的路径长为 .
【答案】(1)2![]() ;BE2+CD2=4AD2;(2)能满足(1)中的结论,见解析;(3)2
;BE2+CD2=4AD2;(2)能满足(1)中的结论,见解析;(3)2![]()
【解析】
(1)依据旋转性质可得:DE=DA=CD,∠BDE=∠ADB=60°,再证明:△BDE≌△BDA,利用勾股定理可得结论;
(2)将△ACD绕点A顺时针旋转120°得到△ABD′,再证明:∠D′BE=∠D′AE=90°,利用勾股定理即可证明结论仍然成立;
(3)从(2)中发现:∠CBE=30°,即:点D运动路径是线段;分别求出点D位于D1时和点D运动到M时,对应的BE长度即可得到结论.
解:(1)如图1,∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵AD=DC
∴∠CAD=∠ACB=30°,∠ADB=∠CAD+∠ACB=60°,
∴∠BAD=90°,
由旋转得:DE=DA=CD,∠BDE=∠ADB=60°
∴△BDE≌△BDA(SAS)
∴∠BED=∠BAD=90°,BE=AB=![]()
∴BE2+CD2=BE2+DE2=BD2
∵![]() =cos∠ADB=cos60°=
=cos∠ADB=cos60°=![]()
∴BD=2AD
∴BE2+CD2=4AD2;
故答案为:![]() ;BE2+CD2=4AD2;
;BE2+CD2=4AD2;
(2)能满足(1)中的结论.如图2,将△ACD绕点A顺时针旋转120°得到△ABD′,使AC与AB重合,
∵∠DAD′=120°,∠BAD′=∠CAD,∠ABD′=∠ACB=30°,AD′=AD=DE,∠DAE=∠AED=30°,BD′=CD,∠AD′B=∠ADC
∴∠D′AE=90°
∵∠ADB+∠ADC=180°
∴∠ADB+∠AD′B=180°
∴A、D、B、D′四点共圆,
同理可证:A、B、E、D四点共圆,A、E、B、D′四点共圆;
∴∠D′BE=90°
∴BE2+BD′2=D′E2
∵在△AD′E中,∠AED′=30°,∠EAD′=90°
∴D′E=2AD′=2AD
∴BE2+BD′2=(2AD)2=4AD2
∴BE2+CD2=4AD2.
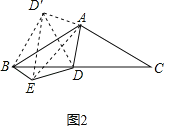
(3)由(2)知:经过B、E、D三点的圆必定经过D′、A,且该圆以D′E为直径,
该圆最小即D′E最小,∵D′E=2AD
∴当AD最小时,经过B、E、D三点的圆最小,此时,AD⊥BC
如图3,过A作AD1⊥BC于D1,∵∠ABC=30°
∴BD1=ABcos∠ABC=![]() cos30°=3,AD1=
cos30°=3,AD1=![]()
∴D1M=BD1﹣BM=3﹣1=2
由(2)知:在D运动过程中,∠CBE=30°,∴点D运动路径是线段;
当点D位于D1时,由(2)中结论得:![]() ,∴BE1=
,∴BE1=![]()
当点D运动到M时,易求得:BE2=![]()
∴E点经过的路径长=BE1+BE2=2![]()
故答案为:2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
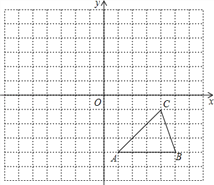
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会提出了要坚定实施七大战略,某数学兴趣小组从中选取了四大战略进行调查,A:科教兴国战略,B:人才强国战略,C:创新驱动发展战略,D:可持续发展战略,要求被调查的每位学生只能从中选择一个自已最关注的战略,根据调查结果,该小组绘制了如图所示的两幅不完整的统计图,请你根据统计图中提供的信息,解答下列问题:
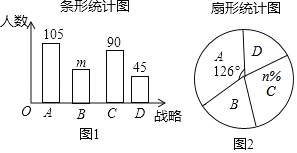
(1)求本次抽样调查的学生人数;
(2)求出统计图中m、n的值;
(3)在扇形统计图中,求战略B所在扇形的圆心角度数;
(4)若该校有3000名学生,请估计出选择战略A和B共有的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C是圆上的点,D是优弧ABC的中点.
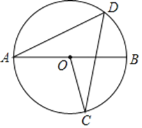
(1)若∠AOC=100°,则∠D的度数为 ,∠A的度数为 ;
(2)求证:∠ADC=2∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,将四边形
上,将四边形![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 、
、![]() 的对称点分别记为
的对称点分别记为![]() 、
、![]() .
.
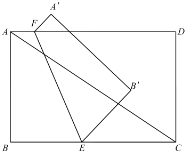
(1)当![]() 时,若点
时,若点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的长;
的长;
(2)设![]() ,若翻折后存在点
,若翻折后存在点![]() 落在线段
落在线段![]() 上,则
上,则![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
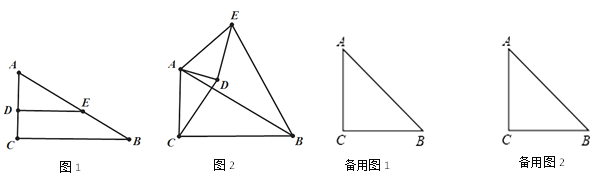
【题目】如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=![]() 时,
时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=![]() 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2
时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2![]() ,求线段CD的长.
,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
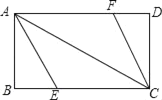
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com