
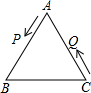
 如图,在△ABC中,AB=6cm,AC=5cm,点P从A点出发,以2cm/S的速度沿AB方向向B运动,同时点Q从C点出发,以1cm/S的速度沿CA方向向点A运动,当一点到达终止,当一点也停止,连接PQ.设运动时间为ts,当t=$\frac{15}{8}$或$\frac{25}{17}$S时,△ABC与△APQ相似.
如图,在△ABC中,AB=6cm,AC=5cm,点P从A点出发,以2cm/S的速度沿AB方向向B运动,同时点Q从C点出发,以1cm/S的速度沿CA方向向点A运动,当一点到达终止,当一点也停止,连接PQ.设运动时间为ts,当t=$\frac{15}{8}$或$\frac{25}{17}$S时,△ABC与△APQ相似. 分析 根据题意得:AP=2tcm,CQ=tcm,则AQ=(5-t)cm,分两种情况:①当$\frac{AP}{AB}=\frac{AQ}{AC}$时,$\frac{2t}{6}=\frac{5-t}{5}$,解方程即可;
②当$\frac{AP}{AC}=\frac{AQ}{AB}$时,$\frac{2t}{5}=\frac{5-t}{6}$,解方程即可;即可得出结果.
解答 解:根据题意得:AP=2tcm,CQ=tcm,则AQ=(5-t)cm,
∵∠A=∠A,
∴分两种情况:
①当$\frac{AP}{AB}=\frac{AQ}{AC}$时,$\frac{2t}{6}=\frac{5-t}{5}$,
解得:t=$\frac{15}{8}$;
②当$\frac{AP}{AC}=\frac{AQ}{AB}$时,$\frac{2t}{5}=\frac{5-t}{6}$,
解得:t=$\frac{25}{17}$;
综上所述:t=$\frac{15}{8}$s或$\frac{25}{17}$s时,△ABC与△APQ相似;
故答案为:$\frac{15}{8}$或$\frac{25}{17}$.
点评 本题考查了相似三角形的判定方法、解方程;熟练掌握相似三角形的判定方法,由两边成比例得出方程是解决问题的关键;注意分类讨论.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你在方格纸上按照如下要求设计直角三角形,所作三角形的各个顶点均在格点上:
请你在方格纸上按照如下要求设计直角三角形,所作三角形的各个顶点均在格点上:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -22=4 | B. | $\frac{2^2}{3}=\frac{4}{9}$ | C. | $({-3.5})-({-5\frac{1}{2}})=2$ | D. | $({-\frac{1}{2}})-|{-\frac{1}{2}}|=0$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{a}-\sqrt{b}$ | B. | $\sqrt{a}+\sqrt{b}$ | C. | $\frac{{\sqrt{a}-\sqrt{b}}}{a-b}$ | D. | $\frac{{\sqrt{a}+\sqrt{b}}}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com