
分析 (1)根据有理数的乘法分配律,可得答案;
(2)根据有理数的混合运算,可得答案;
(3)根据度分秒的加法,可得答案;
(4)根据去括号、合并同类项,可化简整式,根据代数式求值,可得答案.
解答 解:(1)原式=$\frac{7}{12}$×36-$\frac{1}{2}$×36-$\frac{5}{6}$×36=21-18-30=-27;
(2)原式=-9+(-8)×$\frac{1}{2}$=-9+(-4)=-13;
(3)原式=81°77′=82°17′;
(4)=-a2+6ab-9+2a2+8ab-9
=a2+14ab-18,
当a=-$\frac{2}{3}$,b=6时,
原式=(-$\frac{2}{3}$)2+14×(-$\frac{2}{3}$)×6-18
=$\frac{4}{9}$-56-18
=-73$\frac{5}{9}$.
点评 本题考查了度分秒的换算、有理数的运算、整式的加减,熟记法则并根据法则计算是解题关键.


科目:初中数学 来源: 题型:解答题
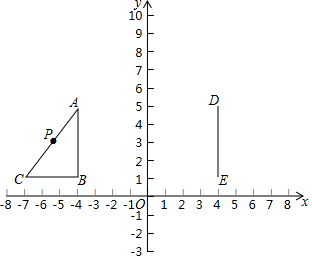 如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).
如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
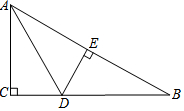 如图,在 Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=2,则DE的长为( )
如图,在 Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=2,则DE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠α的补角和∠β的补角相等 | B. | ∠α的余角和∠β的补角相等 | ||
| C. | ∠α的余角和∠β的补角互余 | D. | ∠α的余角和∠β的补角互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2500(1+x)+2500(1+x)2=3600 | B. | 2500(1+x%)2=3600 | ||
| C. | 2500x2=3600 | D. | 2500(1+x)2=3600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com