
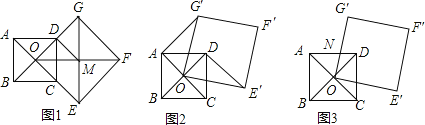
【题目】如图,点O是正方形ABCD两条对角线的交点,分别延长CO到点G,OC到点E,使OG=2OD、OE=2OC,然后以OG、OE为邻边作正方形OEFG.
(1)如图1,若正方形OEFG的对角线交点为M,求证:四边形CDME是平行四边形.
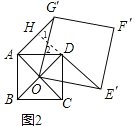
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,如图2,连接AG′,DE′,求证:AG′=DE′,AG′⊥DE′;
(3)在(2)的条件下,正方形OE′F′G′的边OG′与正方形ABCD的边相交于点N,如图3,设旋转角为α(0°<α<180°),若△AON是等腰三角形,请直接写出α的值.
【答案】(1)证明见解析;(2)证明见解析;(3)α的值是22.5°或45°或112.5°或135°或157.5°.
【解析】
(1)由四边形OEFG是正方形,得到ME=![]() GE,根据三角形的中位线的性质得到CD∥GE,CD=
GE,根据三角形的中位线的性质得到CD∥GE,CD=![]() GE,求得CD=GE,即可得到结论;
GE,求得CD=GE,即可得到结论;
(2)如图2,延长E′D交AG′于H,由四边形ABCD是正方形,得到AO=OD,∠AOD=∠COD=90°,由四边形OEFG是正方形,得到OG′=OE′,∠E′OG′=90°,由旋转的性质得到∠G′OD=∠E′OC,求得∠AOG′=∠COE′,根据全等三角形的性质得到AG′=DE′,∠AG′O=∠DE′O,即可得到结论;
(3)分类讨论,根据三角形的外角的性质和等腰三角形的性质即可得到结论.
(1)证明:∵四边形OEFG是正方形,
∴ME=![]() GE,
GE,
∵OG=2OD、OE=2OC,
∴CD∥GE,CD=![]() GE,
GE,
∴CD=GE,
∴四边形CDME是平行四边形;
(2)证明:如图2,延长E′D交AG′于H,
∵四边形ABCD是正方形,
∴AO=OD,∠AOD=∠COD=90°,
∵四边形OEFG是正方形,
∴OG′=OE′,∠E′OG′=90°,
∵将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,
∴∠G′OD=∠E′OC,
∴∠AOG′=∠COE′,
在△AG′O与△ODE′中,
 ,
,
∴△AG′O≌△ODE′
∴AG′=DE′,∠AG′O=∠DE′O,
∵∠1=∠2,
∴∠G′HD=∠G′OE′=90°,
∴AG′⊥DE′;
(3)①正方形OE′F′G′的边OG′与正方形ABCD的边AD相交于点N,如图3,
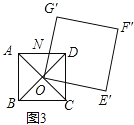
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO-∠ADO=22.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°-45°=45°;
②正方形OE′F′G′的边OG′与正方形ABCD的边AB相交于点N,如图4,
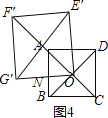
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO+90°=112.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°+45°=135°,
Ⅲ、当AN=AO时,旋转角a=∠ANO+90°=67.5+90=157.5°,
综上所述:若△AON是等腰三角形时,α的值是22.5°或45°或112.5°或135°或157.5°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
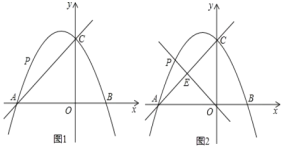
【题目】在平面直角坐标系中,抛物线y=-![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的表达式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE∶OE=3∶8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备开设特色活动课,各科目的计划招生人数和报名人数,列前三位的如下表所示:
科目 | 小制作 | 足球 | 英语口语 |
计划人数 | 100 | 90 | 60 |
科目 | 小制作 | 英语口语 | 中国象棋 |
报名人数 | 280 | 250 | 200 |
若计划招生人数和报名人数的比值越大,表示学校开设该科目相对学生需要的满足指数就越高.那么根据以上数据,满足指数最高的科目是( )
A. 足球B. 小制作C. 英语口语D. 中国象棋
查看答案和解析>>
科目:初中数学 来源: 题型:
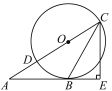
【题目】如图,CD是⊙O的直径,CB是⊙O的弦,点A在CD的延长线上,过点C作CE⊥AB,交AB的延长线于点E,且CB平分∠ACE.
(1)求证:直线AB是⊙O的切线;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
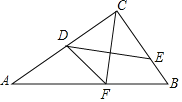
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别在AC、BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处,若AC=12,AB=13,则CD的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个点的纵坐标恰好是横坐标![]() 倍,那么我们就把这个点定义为“萌点”.
倍,那么我们就把这个点定义为“萌点”.
(1)若点![]() 的坐标分别为
的坐标分别为![]() ,则四边形
,则四边形![]() 四条边上的“萌点”坐标是___.
四条边上的“萌点”坐标是___.
(2)若一次函数![]() 的图像上有一个“萌点”的横坐标是-3,求k值;
的图像上有一个“萌点”的横坐标是-3,求k值;
(3)若二次函数![]() 的图像上没有“萌点”,求k的取值范围.
的图像上没有“萌点”,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,顶点为
,顶点为![]() .
.

(1)求这条抛物线表达式;
(2)将该抛物线向右平移,平移后的新抛物线顶点为![]() ,它与
,它与![]() 轴交点为
轴交点为![]() ,联结
,联结![]() 、
、![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的正切值;
的正切值;
(3)联结![]() ,在(2)的条件下,射线
,在(2)的条件下,射线![]() 平分
平分![]() ,求点
,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以901班学生的体育测试成绩为样本,按A.B.C.D四个等级进行统计,并将结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(A级:90分及以上;B级:75分~89分;C级:60分~74分;D级:60分以下.注:分数均为整数值)
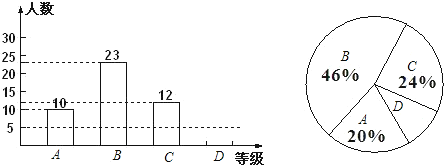
(1)请把条形统计图补充完整;
(2)求样本中D级的学生人数占全班学生人数的百分比;
(3)求扇形统计图中A级所在的扇形的圆心角度数;
(4)若该校九年级有400名学生,且75分及以上记为“满分”,请你用此样本估计该校体育测试中获得“满分”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.
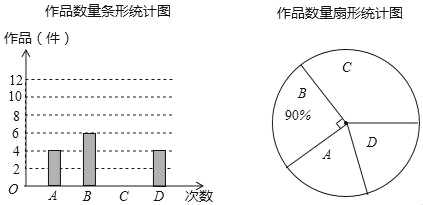
请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com