
如图1,在等腰△ABC中,底边BC=8,高AD=2,一动点Q从B点出发,以每秒1个单位的速度沿BC向右运动,到达D点停止;另一动点P从距离B点1个单位的位置出发,以相同的速度沿BC向右运动,到达DC中点停止;已知P、Q同时出发,以PQ为边作正方形PQMN,使正方形PQMN和△ABC在BC的同侧,设运动的时间为t秒(t≥0).
(1)当点N落在AB边上时,t的值为 ,当点N落在AC边上时,t的值为 ;
(2)设正方形PQMN与△ABC重叠部分面积为S,求出当重叠部分为五边形时S与t的函数关系式以及t的取值范围;
(3)(本小题选做题,做对得5分,但全卷不超过150分)
如图2,分别取AB、AC的中点E、F,连接ED、FD,当点P、Q开始运动时,点G从BE中点出发,以每秒 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
(1)1 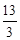
(2) 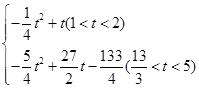
(3)可能.t=0或t=2或4≤t≤5
解析试题分析:本题属于学科综合题,代数知识与几何知识有机结合在一起,体现了数形结合的思想,解答此类综合题关键是数与形的灵活转化.(1)当点N落在AB边上时,NP=1,NP∥AD,利用平行线对应线段成比例的性质可算出t的值;当N落在AC边上时,正方形的边长不再是1,Q点已经停在D点,PD=t-3,∴PN="t-3," PC=4-(t-3)=7-t ∵PN∥DA ∴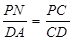 ∴
∴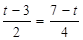 ∴t=
∴t=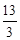 .(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合.
.(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合.
试题解析: (1)解:∵NP∥AD PN=1 AD="2" ∴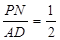 ∴PN是△ABD的中位线 ∴BP=2∴t=1
∴PN是△ABD的中位线 ∴BP=2∴t=1
∵PD="t-3," ∴PN="t-3," PC=4-(t-3)=7-t
∵PN∥DA ∴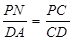 ∴
∴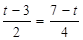 ∴t=
∴t=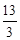 .
.
( 2 )当 0<t<1,重叠部分为梯形,当1<t<2时,设EQ交AB于R,则重叠部分为五边形PQREN.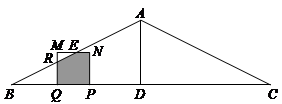
(2)当1<t<2时, 设EQ交AB于R,则重叠部分为五边形PQREN.
∵ME=2-t,MR= ME=
ME= (2-t)∴S△MRE =
(2-t)∴S△MRE = ME·MR=
ME·MR=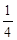 (2-t)2
(2-t)2
∴S=S正方形PQMN-S△MRE =1-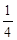 (2-t)2=-
(2-t)2=-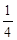 t2+t
t2+t 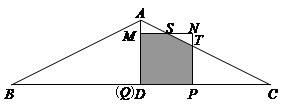
当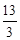 <t<5时
<t<5时
设MN交AC于S,PN交AC于T,则重叠部分为五边形PQMST
∵AM=2-(t-3)=5-t,MS=2AM=2(5-t) PC=7-t,PT= PC=
PC= (7-t)
(7-t)
∴S△AMS = AM·MS=(5-t)2,S△PTC =
AM·MS=(5-t)2,S△PTC = PC·PT=
PC·PT=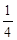 (7-t)2
(7-t)2
又S△ADC = AD·CD=
AD·CD= ×2×4=4
×2×4=4
∴S=S△ADC-S△AMS -S△PTC =4-(5-t)2-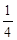 (7-t)2=-
(7-t)2=-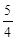 t2+
t2+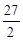 t-
t-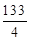
综上所述,当重叠部分为五边形时S与t的函数关系式为: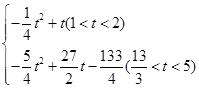
(3)可能. t=0或t=2或4≤t≤5
当t=0时,QP=1,GP= ,G为BE中点,也为NP中点.
,G为BE中点,也为NP中点.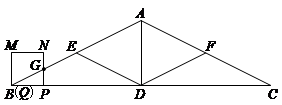
当t=2时,G点所走路程为 ×2=
×2= ,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP=
,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP= NP为NP中点.
NP为NP中点.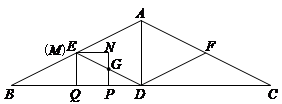
当4≤t≤5时,DP=t-3 设NP与DF相交与点R则PR= (t-3) 由勾股定理得DR=
(t-3) 由勾股定理得DR= (t-3) 此时DG=
(t-3) 此时DG= t-
t-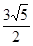 =
= (t-3) 所以点R与点G重合.
(t-3) 所以点R与点G重合.
考点:1、三角形相似;2、二次函数;3、动点型的图形面积;4、探究型试题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和( ,
, )两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
(1)求a,b,c的值;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2 + bx + c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3)。
(1)求抛物线y= ax2 + bx + c 的解析式;
(2)求△AOC和△BOC的面积比;
(3)在对称轴上是否存在一个P点,使△PAC的周长最小。若存在,请你求出点P的坐标;若不存在,请你说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
复习课中,教师给出关于x的函数 (k是实数).
(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当 时,不是y随x的增大而增大就是y随x的增大而减小;
时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;
教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线经过A(-1,0),B(5,0),C(0,?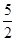 )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.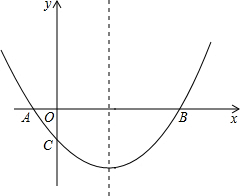
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为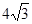 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.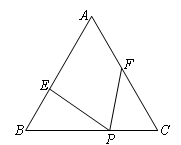
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com