
【题目】已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.
(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=![]() ∠BOD,求∠DOE的度数;
∠BOD,求∠DOE的度数;
(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O点从OB开始以5度秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC时,求t的值:
(3)若射线OM绕着O点从OA开始以15度秒的速度逆时针旋转至OB结束,在旋转过程中,ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于180°的角)

【答案】(1)35°.(2)当∠EOC=∠FOC时,t=3s或7.5s.(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.当4<t<12时,2∠BON﹣∠BOM=210°.
【解析】
(1)根据∠EOD=∠EOB﹣∠DOB,只要求出∠EOB,∠DOB即可;
(2)分两种情形列出方程即可解决问题;
(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.②当4<t<12时,2∠BON﹣∠BOM=210°.用t表示∠BON、∠BOM,求2∠BON一∠BOM的值即可;
解:(1)∵∠AOB=150°,OE平分∠AOB,
∴∠EOB=![]() ∠AOB=75°,
∠AOB=75°,
∵∠BOC=60°,∠COD=![]() ∠BOD,
∠BOD,
∴∠BOD=40°,∠COD=20°,
∴∠EOD=∠EOB﹣∠DOB=75°﹣40°=35°.
(2)当OE在∠AOC内部时,∵∠EOC=∠FOC,
∴90﹣15t=60﹣5t,
∴t=3.
当OE与OF重合时,15t+5t=150°,
t=7.5.
综上所述,当∠EOC=∠FOC时,t=3s或7.5s.
(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.
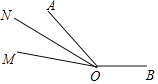
理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=150°+7.5t,∠BOM=150°+15t,
∴2∠BON一∠BOM=2(150°+7.5t)﹣(150°+15t)=150°
②当4<t<12时,2∠BON﹣∠BOM=210°.
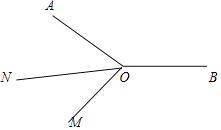
理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=210°﹣7.5t,∠BOM=210°﹣15t,
∴2∠BON一∠BOM=2(210°﹣7.5t)﹣(210°﹣15t)=210°(4<t<12).


科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE垂直平分BC,垂足为点D,交AB于点E,且AD=AC,EC交AD于点F,下列说法:
①△ABC∽△FDC;②点F是线段AD的中点;③S△AEF:S△AFC=1:4;④若CE平分∠ACD,则∠B=30°,其中正确的结论有_____(填写所有正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
操作次数 | 1 | 2 | 3 | 4 | … |
正方形个数 | 4 | 7 |
|
| … |
(1)如果剪100次,共能得到 个正方形;
(2)如果剪n次共能得到bn个正方形,试用含有n、bn的等式表示它们之间的数量关系 ;
(3)若原正方形的边长为1,设an表示第n次所剪的正方形的边长,试用含n的式子表示an ;
(4)试猜想a1+a2+a3+a4+…+an﹣1+an与原正方形边长的数量关系,并用等式写出这个关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厉害了,我的国!2018年10月24日,连接香港、珠海、澳门三座城市的港珠澳大桥建成通车.这座全长55公里,投资约1269亿元,经过6年筹备与9年建设的跨海大桥,创造了400多项专利和七项世界之最,被誉为世界的第七大奇迹.全国工程勘察设计大师、港珠澳大桥总设计师孟凡超表示“港珠澳大桥建成,标志着我国由桥梁大国向桥梁强国迈进.”请用科学记数法表示港珠澳大桥的总投资额( )
A.12.69×10![]() 亿元B.1.269×10
亿元B.1.269×10![]() 元
元
C.1.269×10![]() 元D.1.269×10
元D.1.269×10![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,点C在数轴上对应的数为c,且|a+2|+(b﹣1)2=0,2c﹣1=![]() c+2.
c+2.
![]()
(1)求线段AB的长;
(2)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由.
(3)现在点A,B,C开始在数轴上运动,若点A以每秒1个单位长度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动.假设t秒后,点B和点C之间的距离表示为BC,点A和点B之间的距离表示为AB.请问AB﹣BC的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求出常数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为![]() ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届全国青年运动会将于2019年8月在太原开幕,这是山西历史上第一次举办全国大型综合性运动会,必将推动我市全民健康理念的提高.某体育用品商店近期购进甲、乙两种运动衫各50件,甲种用了2000元,乙种用了2400元.商店将甲种运动衫的销售单价定为60元,乙种运动衫的销售单价定为88元.该店销售一段时间后发现,甲种运动衫的销售不理想,于是将余下的运动衫按照七折销售;而乙种运动衫的销售价格不变.商店售完这两种运动衫至少可获利2460元,求甲种运动衫按原价销售件数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com