
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
【答案】(1)该方程有两个实数根;
(2)等腰三角形的周长为7或8,面积为![]() 或2
或2![]() .
.
【解析】分析:(1)根据方程的系数结合根的判别式,可得出△=(2k-3)2≥0,由此即可得出该方程有两个实数根;
(2)分3为底边长及腰长两种情况考虑:①当3为底边长是,由△=0可求出k值,将其代入原方程可求出三角形的腰长,再根据周长及面积公式可求出等腰三角形的周长及面积;②当3为腰长时,将x=3代入原方程可求出k值,代入k值可求出等腰三角形的底边长度,再根据周长及面积公式可求出等腰三角形的周长及面积.综上即可得出结论.
详解:(1)∵△=[-(2k+1)]2-4×4(k-![]() )=4k2-12k+9=(2k-3)2≥0,
)=4k2-12k+9=(2k-3)2≥0,
∴该方程有两个实数根;
(2)①当3为底边长时,△=(2k-3)2=0,
∴k=![]() ,
,
此时原方程为x2-4x+4=0,
解得:x1=x2=2.
∵2、2、3能组成三角形,
∴三角形的周长为2+2+3=7,三角形的面积为![]() ×3×
×3×![]()
=![]() ;
;
②当3为腰长时,将x=3代入原方程,得:9-3×(2k+1)+4(k-![]() )=0,
)=0,
解得:k=2,
此时原方程为x2-5x+6=0,
解得:x1=2,x2=3.
∵2、3、3能组成三角形,
∴三角形的周长为2+3+3=8,三角形的面积为![]() ×2×
×2×![]() .
.
综上所述:等腰三角形的周长为7或8,面积为![]() 或
或![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
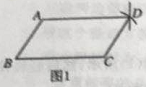
【题目】盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证
已知:如图1,在四边形ABCD中,BC=AD,________________________
求证:________________________
(1)填空,补全已知和求证
(2)按盈盈的想法写出证明
(3)用文字叙述所证命题的逆命题为________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). 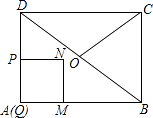
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
①a=40,m=1;
②乙的速度是80km/h;
③甲比乙迟 ![]() h到达B地;
h到达B地;
④乙车行驶 ![]() 小时或
小时或 ![]() 小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
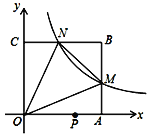
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() 分别相交于
分别相交于![]() 两点,
两点,![]() 的面积为10.若动点
的面积为10.若动点![]() 在
在![]() 轴上,则
轴上,则![]() 的最小值是_____________
的最小值是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两条对角线AC、BD相交于点O,延长BA至点F,使BF=AC,连接DF,∠DBA的平分线交DF于点P,连接PA.PO,如果AB=![]() ,那么PA2+PO2=______.
,那么PA2+PO2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣ ![]() x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 . 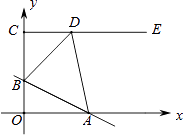
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com