
【题目】如图,BD是正方形ABCD的对角线,BC=4,边BC在其所在的直线上平移,平移后得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
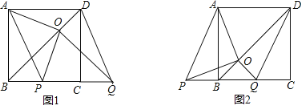
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并利用图1加以证明.
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤4),求y与x之间的函数关系式,并求出y的最大值.
【答案】(1)平行四边形(2)OA=OP,OA⊥OP,理由见解析(3)当P点在B点右侧时,y=![]() (x+2)21;当P点在B点左侧时,y=
(x+2)21;当P点在B点左侧时,y=![]() (x2)2+1;当x=4时,y有最大值为8.
(x2)2+1;当x=4时,y有最大值为8.
【解析】
(1)根据平移的性质,可得PQ,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据正方形的性质,平移的性质,可得PQ与AB的关系,根据等腰直角三角形的判定与性质,可得∠PQO,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得到答案.
(1)四边形APQD为平行四边形,
理由如下:
∵四边形ABCD是正方形,
∴AD![]() BC,
BC,
∵边BC在其所在的直线上平移,平移后得到的线段记为PQ,
∴![]()
∴四边形APQD为平行四边形;
(2)OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,

∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(3)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
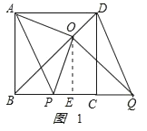
则BQ=x+4,OE=![]() ,
,
∴y=![]() ×
×![]() x,即y=
x,即y=![]() (x+2)21,
(x+2)21,
又∵0≤x≤4,
∴当x=4时,y有最大值为8;
②如图2,当P点在B点左侧时,
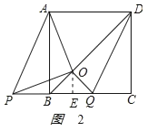
则BQ=4x,OE=![]() ,
,
∴y=![]() ×
×![]() x,即y=
x,即y=![]() (x2)2+1,
(x2)2+1,
又∵0≤x≤4,
∴当x=2时,y有最大值为1;
综上所述,∴当x=4时,y有最大值为8.


科目:初中数学 来源: 题型:
【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
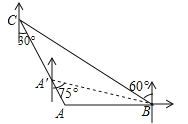
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点为D的抛物线y=﹣x2+bx+c交x轴于A、B(3,0),交y轴于点C,直线y=﹣![]() x+m经过点C,交x轴于E(4,0).
x+m经过点C,交x轴于E(4,0).
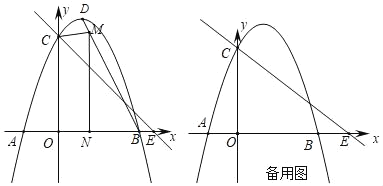
(1)求出抛物线的解析式;
(2)如图1,点M为线段BD上不与B、D重合的一个动点,过点M作x轴的垂线,垂足为N,设点M的横坐标为x,四边形OCMN的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点P为x轴的正半轴上一个动点,过P作x轴的垂线,交直线y=﹣![]() x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
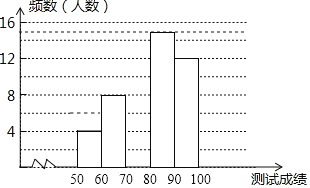
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
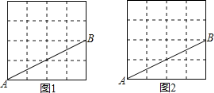
(1)在图1中画出以AB为底边的等腰直角三角形ABC,点C在小正方形的顶点上;
(2)在图2中画出以AB为腰的等腰三角形ABD,点D在小正方形的顶点上,且△ABD的面积为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,点G在边
,点G在边![]() 上,连接
上,连接![]() ,作
,作![]() 于点E,
于点E,![]() 于点F,连接
于点F,连接![]() 、
、![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
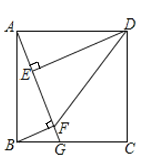
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若点G从点B沿![]() 边运动至点C停止,求点E,F所经过的路径与边
边运动至点C停止,求点E,F所经过的路径与边![]() 围成的图形的面积.
围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() ,点D落在线段AB上,连接BE.
,点D落在线段AB上,连接BE.

(1)求证:DC平分![]() ;
;
(2)试判断BE与AB的位置关系,并说明理由:
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
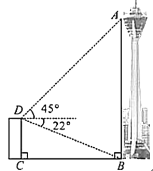
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
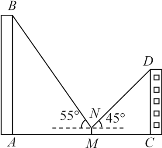
【题目】如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com