
| A. | x≠2 | B. | x≥2 | C. | x≤2 | D. | x>2 |
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
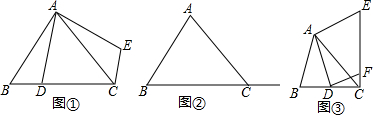
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
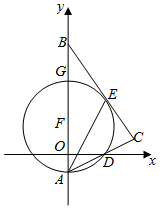 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
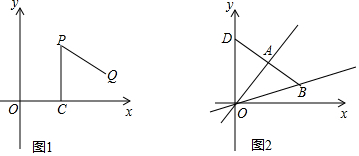
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
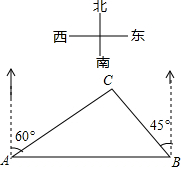 如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).
如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com